Indices for Political-Institutional Analysis (Politometrics)

LOGOS GEOPOLITICAL INSTITUTE
contact@geopolitical-institute.com.br
Brazil, São Paulo/SP – July 19, 2024

ABSTRACT

This article compiles and studies classic indices of political institutional analysis. It does not present new approaches but rather brings together classic indexes and other new ones with conceptual impact, making it possible to carry out a quick and effective consultation on concepts and examples, aimed at students and professionals. There are a total of 28 approaches, all of them with examples and conceptual explanation and how to carry out and interpret each of the results obtained. Emphasis was placed on the explanation regarding the constitution of the equation that forms each of the indices, explaining its structure, to prevent the reader from not understanding the presented format of the equation.

Keywords: Political Institutional Analysis; Political Institutional Index; Government Performance

1. Introduction

This article does not aim to present something authorial, innovative, or unique, but rather to present, in a single work, the classic indices used to analyze institutional policy and others recently presented that have conceptual relevance and impact on the analyses. There are a total of 28 different approaches, some indicators with variations.

The idea is to condense the concepts and equations with brief explanations sufficient to understand the differences and practical applications between the most varied indicators. No in-depth analyses are carried out for the indices, we limit ourselves to presenting the general aspects. The advantage of this article is having the main indexes with the most relevant information, providing a broad overview of the most varied existing approaches.

2: Preliminary Aspects

Some preliminary elements are necessary to facilitate the reading of this article. We then present these points that precede the study of indices and other indicators.

2.1 – List of acronyms

For organizational purposes, we present the acronyms used in this article.

A: Number of abstentions from votes in a legislative house
d: Number of times the parliamentarian followed the party’s guidance when voting in the legislative house
gov_n: All votes that were not in agreement with the government in the legislative house
gov_y: Number of votes in agreement with the government in the legislative house
i: Counter of the number of parties, and others
m: Proportion of ministries that the party won
MIL: Relative number of active military personnel, in base 1000
n: Total number of parties
N: Number of “no” votes in a legislative house, in percentage values
nd: Number of times the parliamentarian did not follow the party’s guidance when voting in the legislative house
O: Number of times the party instructed parliamentarians to vote in the legislative house
p: Proportion of seats in the legislative house occupied by the party
P: Number of seats in the legislative house occupied by the party
GDPM: Relative military expenditure in base 1000 and terms of GDP, in a given year
S: Relative area of ​​the territory, in base 1000, in km²
T: Total number of seats in the legislative house
v: Proportion of votes received by the party
V: Number of votes received by the party
V⁺: Number of surplus votes received in an election
V^–: Number of votes lost in an election (without conversion into seats)
Y: Number of “yes” votes in a legislative house, in percentage values
Z: Total number of votes in the election

2.2: Input Data

We are making available the data that will be used in the examples of each indicator.

i	Votos Vi	vi	Vi%	Pi	Pi%
1	27.200.000	0,2720	27,20	60	24,74
2	24.500.000	0,2450	24,50	55	23,73
3	20.040.000	0,2040	20,40	42	22,22
4	7.600.000	0,0760	7,60	12	9,09
5	6.300.000	0,0630	6,30	9	7,07
6	5.900.000	0,0590	5,90	8	6,06
7	2.900.000	0,0290	2,90	6	4,04
8	2.400.000	0,0240	2,40	3	1,51
9	1.900.000	0,0190	1,90	2	1,01
10	900.000	0,009	0,9	1	0,5
n = 10	Z = 100.000.000	Σvi = 1	ΣVi% = 100	T = 98	ΣPi% = 100

i	Pi	pi	pi2	vi	vi2	(vi-pi)	(vi-pi)2
1	60	0,247474 (= 49/198)	0,061243	0,2720	0,073984	0,024526	0,0006031
2	55	0,237373 (= 47/198)	0,056345	0,2450	0,060025	0,007627	0,0000581
3	42	0,222222 (= 44/198)	0,0493826	0,2040	0,041616	-0,18222	0,0332041
4	12	0,090909 (= 18/198)	0,0082464	0,0760	0,005776	-0,02309	0,0005331
5	9	0,070707 (= 14/198)	0,0049994	0,0630	0,003969	-0,01407	0,0001979
6	8	0,060606 (= 12/198)	0,0036730	0,0590	0,003481	0,05294	0,0028026
7	6	0,040404 (= 8/198)	0,0016324	0,0290	0,000841	-0,01140	0,0001299
8	3	0,015151 (= 3/198)	0,0002295	0,0240	0,000576	0,008849	0,0000783
9	2	0,010101 (= 2/198)	0,0001020	0,0190	0,000361	0,008899	0,0000791
10	1	0,005051 (= 1/198)	0,000025	0,009	0,000081	0,003949	0,0000155
n = 10	T = 198	Σpi = 1	Σ(pi)2 = 0,18587	Σvi = 1	Σ(vi)2 = 0,19071	Σ|vi-pi| =0,33757	Σ|vi-pi|2 =0,03770

i	Vi%	Pi%	Vi% – Pi%	(Vi% – Pi%)2	(Vi% – Pi%)2/Vi%
1	27,20	24,74	2,46	6,0516	0,2224853
2	24,50	23,73	0,77	0,5929	0,0242000
3	20,40	22,22	-1,82	3,3124	0,1623725
4	7,60	9,09	-1,49	2,2201	0,2921184
5	6,30	7,07	-0,77	0.5929	0,0941111
6	5,90	6,06	-0,16	0,0256	0,0043389
7	2,90	4,04	-1,14	1,2996	0,4481379
8	2,40	1,51	0,89	0,7921	0,3300416
9	1,90	1,01	0,89	0,7921	0,4168947
10	0,9	0,5	0,4	0,16	0,1777777
n = 10	ΣVi% = 100	ΣPi% = 100	—	—	Σ= 2,17247

Candidate	Votes – Election 1	Votes – Election 2
A	60.000.000	60.000.000
B	31.000.000	31.000.000
C	7.000.000	7.000.000
D	1.100.000	—
E	900.000	—
Total	100.000.000	98.000.000

Election	Year	Party A (1980)	Party B (1982)	Party C (1994)	Party D (2004)	Party E (2005)	Total
1	1994	51,2%	44,3%	4,5%	—	—	100%
2	1998	46,8%	42,4%	10,8%	—	—	100%
3	2000	30,4%	42,1%	27,5%	—	—	100%
4	2003	27,2%	38,5%	34,3%	—	—	100%
5	2004	36,2%	31,7%	29,2%	2,9%	—	100%
6	2008	29,4%	32,9%	33,0%	1,8%	2,9%	100%
7	2010	15,9%	36,7%	42,5%	1,7%	3,2%	100%
8	2012	30,1%	7,8%	58,3%	2,3%	1,5%	100%
9	2016	35,6%	21,5%	37,8%	2,3%	2,8%	100%
10	2020	32,0%	29,5%	35,2%	1,1%	2,2%	100%

Parliamentarian/Party	Vote 1	Vote 2	Vote 3	Vote 4	Vote 5	Vote 6	Votes %
A (-)	+1	0	+1	-1	+1	0	27,3
B (+)	+1	0	+1	+1	+1	0	24,3
C (-)	+1	0	-1	+1	+1	0	19,8
D (+)	-1	0	+1	+1	-1	0	9,8
E (+)	+1	0	+1	+1	-1	0	6,2
F (-)	-1	0	+1	-1	-1	0	4,6
G (+)	+1	0	+1	+1	-1	0	4,4
H (-)	+1	0	+1	-1	-1	0	3,6

Year	Ministries
1994	PA: 14; PB: 8; PC: 3; Total ministries: 25
1998	PA: 14; PB: 8; PC: 3; Total ministries: 25
2000	PA: 16; PC: 9; Total ministries: 25
2004	PA: 8; PB: 5; PC: 9; PD: 3; Total ministries: 25
2008	PA: 8; PB: 6; PC: 4; PD: 3; PE: 4; Total ministries: 25
2012	PA: 9; PB: 6; PC: 4; PD: 2; PE: 4; Total ministries: 25
2016	PA: 4; PB: 5; PC: 4; PD: 6; PE: 6; Total ministries: 25
2020	PA: 10; PB: 6; PC: 4; PD: 3; PE: 2; Total ministries: 25

2.3: Classification of Indices

To facilitate understanding, we categorize the analyses and indicators based on the data used and how they are calculated. The classification initially has didactic purposes and can be extended to a more technical analysis, because technical aspects were considered for the presented classification.

For teaching purposes, in our categorization, we have: 1 – Analysis of the Electoral System; 2 – Party System Mobility Analysis; 3 – Analysis of Party Behavior and 4 – Analysis of the Government (Executive). These are divided as follows:

1: Analysis of the Electoral System

A – Weighting Indices
RAE – Party Fragmentation Index
ENP – Effective Number of Parties

B – Linear Deviation Indices
RAE^D – Rae Electoral System Disproportionality Index
LH – Loosemore-Hanby Electoral System Disproportionality Index
RO – Rose Electoral System Proportionality Index
G – Grofman Index of Disproportionality of the Electoral System

C – Quadratic Deviation Indices
LSq – Gallagher Electoral System Disproportionality Index
SL – Sainte-Lagüe Index of Disproportionality of the Electoral System
MO – Monroe Electoral System Disproportionality Index

D – Overrepresented Indices
MD – Maximum Deviation Index of Disproportionality of the Electoral System
LJ – Lijphart Index of Disproportionality of the Electoral System
DH- D’Hont Index of Disproportionality of the Electoral System

E – Measures of Surplus Values
W – Wasted Vote
GAP – Efficiency Gap

2: Party System Mobility Analysis
EV – Pedersen Electoral Volatility Index
LW – Lewis Party Stabilization Index
EDP ​​- Established Party Dominance Index
Tp – Party Age
PI – Party Institutionalization Index
NP – Number of New Parties Criterion

3: Analysis of Party Behavior
D – Party Discipline Index
R – Rice Index of Intraparty Cohesion

4: Government Analysis (Executive)
POL – Percentage Polarization Index
M – Coalescence Rate
GOV – Presidential Support Assessment
ε – Political-Institutional Performance Assessment
X – Party System Closure Index
MW – Military Power Index of a Country

The indicators are presented through these categories and in a chronological manner of emergence, whenever the chronology is relevant in developing new criteria, indices, or indicators.

3: Weighting Indices

These are indices that use the proportion of votes of each party or the proportion of seats won by them in the legislative house.

3.1: RAE Party Fragmentation Index

Proposition: The RAE index was created in 1967, and proposed by Rae (Douglas Whiting Rae; Political Scientist – United States). The index measures party fragmentation in a country. The numerical value can be given as an index, with values ​​between 0 and 1, or it can be presented in percentage form. The first is more common.

Equation: The equation that calculates the RAE index is presented in equation 2. To calculate p_i we use equation 1.

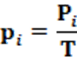
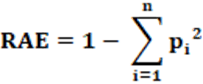
Concepts: Conceptually, the RAE index measures party fragmentation in an election. This is done based on the relative number of party’s legislative seats. Party participation is a global measure. The index considers the participation of each party in a given electoral system based on the legislative seats won by these parties. This means that the RAE index measures how much political representation parties, within a general average, have within this global universe.

This means that the RAE index measures how much political representation all parties if reduced to a single party has. Theoretically, a single party would have 100% political representation, equivalent to saying that fragmentation is zero. In practice, with more than one party, the representation of one party reduces the representation of the others. By doing “an average” it is possible to know how much average representation there would be if this reality were converted to a single party. In other words, the calculation estimates how much representation a single party would have (political strength) if the entire party system were reduced to that single party. For the calculation of the representation, it is possible to reach fragmentation, since one value is complementary to the other.

Now let’s analyze the equation. It has two installments. The portion on the left is number 1 and the portion on the right is the squared sum of the proportions of seats acquired by the parties. The second portion represents, in mathematical terms, party representation (or participation) for the present case.

This idea, present in the second part of the equation, is not exclusive to Political Science and can be seen, for example, in Economics when evaluating the level of competition of companies in a market, which is indicated by the Herfindahl index. Thus, when this value is subtracted from 1, it expresses the opposite, that is, “non-party participation”. In other words, it indicates party fragmentation. A question that may arise is why it is used (p_i)² and not only (p_i). The answer to this is conceptual.

Therefore, we start from the idea that the second part of the equation represents the level of participation of the parties. So, if we use (p_i); the answer turns out to be mathematically incongruent. If (p_i)² we will have, mathematically, a coherent value for analysis. The following examples explain the concept and make the idea clear, based on homogeneous distribution situations. It is important to note that even though it appears that the use of (pi)2 distorts the result, this is not real the result makes sense.

Example situation: Assuming two parties, A and B; where each person has 50% of the seats in the legislative house; What is the party participation of this party system? From this example, if we use (pi) we will have Party A: 0.5; Party B: 0.5. Thus, 0.5 + 0.5 = 1. Therefore, from this calculation, party participation is 1, or 100%, which is wrong because party participation is 50%; since there are two parties and each has 50% of the seats in the legislative house.

When it applies (p_i)² the calculation is as follows: Party A: 0.5; Party B: 0.5. Thus, (0.5)² + (0,5)² = 0.25 + 0.25 = 0.5. Therefore, based on this calculation, party participation is 0.5, or 50%, which is in line with reality; because there are two parties and each has 50% of the legislative seats.

This is replicated for any homogeneous distribution. In other words, regardless of the number of parties and participation (until then, participation with homogeneous distribution), thus the results will always be the same.

For example; in the case of three parties all have 33% of the legislative seats; the result for (p_i) e (p_i)² is respectively; 1 and 0.33; or, 100% and 33%. Using the same logic, for 4 parties and each with 25% of the legislative seats we have, for (p_i) e (p_i)² is, respectively; 1 and 0.25; or, 100% and 25%.

Thus, the calculation using (pi) will always be 1 and if used (p_i)² will always be 1/(number of parties). This doesn’t depend on whether the distribution is homogeneous or not. It is suitable for any distribution and can be extrapolated to heterogeneous distributions, which are more real.

Therefore, the result that interests us is (p_i)² in the second term. This way we have a measure for practical analysis.

Interpretation: The limit values ​​for the RAE index are 0 and 1. When it is 0 (zero) it represents the minimum possible party fragmentation. When it is 1 (one) it represents the maximum possible party fragmentation. Therefore, for values ​​between 0 and 1, we will have the real values. Low values ​​of the RAE index represent low party fragmentation. High values ​​of the RAE index represent high party fragmentation.

Input data: To calculate the RAE index, two pieces of data are needed: The first data necessary is the number of votes obtained by each party (V_i). The second mandatory data is the number of seats of each party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. These values ​​determine the RAE index.

Example: Calculate party fragmentation from the data in Table 02. From Table 02, the calculation of the RAE index is RAE = 1 – Σp². Soon; RAE =1 – 0.18587; which results in RAE = 0.8141; or 81.41%. So, for the example presented, party fragmentation is high.

3.2: Effective Number of Parties – ENP

Proposition: The ENP index was created in 1979, and proposed by Laakso (Markku Laakso; Doctor – Finland) and Taagepera (Rein Taagepera; Political Scientist and Politician – Estonia). The index measures party fragmentation in a country, as the title suggests, and measures the number of parties with real strength within a legislative house. The numerical value can be given as an index, with values ​​between 0 and 1, or it can be presented in percentage form. The first is more common.

Equation: Equation 3 calculates the ENP.

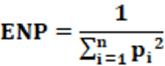
Concepts: Conceptually, it is a number that represents the number of parties that effectively have political power in a legislative house and not an index. Still, from a conceptual point of view, it does not measure party fragmentation in a country, even though it allows this inference, in practice.

The ENP evaluates the effective number of parties in a country. However, if appropriate adaptations are made, it can assess any region, state, or city, for example. Therefore, the ENP is determined based on the relative size of each party based on the number of seats within a given legislative house. In general, the legislative house adopted is the Federal Chamber of Deputies and, in this format, for several purposes, including allowing the comparison of Party Systems between countries, for example.

Interpretation: The ENP indicates the number of parties with real political strength in a country. The ENP is not related to the number of parties but to the number of parties that exercise a certain political force within the legislative house. Finally, some examples will make the idea clearer. Thus, the same number of parties, with different proportions of seats between the parties, changes the value of the ENP. Soon; the ENP measures the number of these parties, which means that strength is seen based on the relative power between the parties.

Low ENP: This occurs in two situations: a) when there are few parties; b) when the distribution is disproportionate when few parties have many legislative seats and many parties have few seats. A low ENP value represents that there are few parties with real political strength, or be, there are one or a few dominant parties in the legislative house, due to the distribution being more disproportionate.

ENP Alto: Similarly, this occurs in two situations: a) when there are many parties; b) when the distribution is more proportional, that is, when the seats are divided more evenly between the parties. Thus, a high ENP value represents that there are many parties with real political strength, that is, that there is not one or a few dominant parties, there is a considerable number of parties with reasonable power in the legislative house due to their more homogeneous relative size.

Mathematically, the ENP informs how many parties have the power in the legislative house to interfere in the approbation, to approve or not approve legislative proposals. In short, the ENP represents the number of parties with real political strength in a region. From the concept, the ENP can vary from 1 to, theoretically, infinity. When ENP = 1 we have the presence of a single dominant party. For different values, ​​we have the number of dominant parties according to the eigenvalue of the ENP.

Input data: The calculation in this article considers the classic idea and uses data from the Federal Chamber of Deputies. In this regard, the only necessary data is the proportion of seats held for each party in the Federal Chamber of Deputies. For this calculation, it’s required to know how many seats each party has and the total number of seats in the legislative house. To do this, we must use equation 1. After performing algebraic manipulations, the ENP value – Effective Number of Parties is obtained.

Example: From Table 2 and equation 3, we have: ENP is worth: ENP = 1/p² = ENP =1/0.18587; therefore ENP = 5.38. But, for the example, the effective number of parties is given by around 4 parties. If we look at the first three parties we see they have a high number of seats compared to the others.

Some examples for interpreting the index: Situation 1: Party 1: 60 seats; Party 2: 2 seats. ENP = 1.066. Situation 2: Party 1: 60 seats; Party 2: 55 seats. ENP = 1.996. In situation 1 the ENP is approximately 1, even with the presence of two parties. In situation 2 there is the same number of parties, however, the distribution of seats is quite homogeneous, resulting in an ENP, of approximately, 2. The explanation for this lies in the distribution of seats between the parties. Soon; in this case, the main factor is the distribution of seats between the parties.

Situation 3: Party 1: 60 seats; Party 2: 55 seats; Party 3: 42 seats; Party 4: 12 seats; Party 5: 9 seats; Party 6: 8 seats; Party 7: 6 seats; Party 8: 3 seats; Party 9: 2 seats; Party 10: 1 seat. ENP = 4.49. Situation 4: Party 1: 60 seats; Party 2: 55 seats; Party 3: 42 seats; Party 4: 50 seats; Party 5: 57 seats; Party 6: 45 seats; Party 7: 55 seats; Party 8: 35 seats; Party 9: 32 seats; Party 10: 46 seats. ENP = 9.66. In this case, we show the strong influence of ENP on the distribution of legislative seats between the parties. In both situations, we have the same number of parties, in this case, 10. However, as the distribution of seats in situation 3 is more disproportionate, the ENP has a value approximate to the number of parties with the largest seats. In situation 4, as the distribution of seats is much more homogeneous, the ENP has a value almost equal to the same number of existing parties. Once again, it is possible to observe that the ENP is a function of the distribution of seats in the legislative house not the number of parties.

Situation 5: Party 1: 60 seats; Party 2: 55 seats; Party 3: 42 seats; Party 4: 12 seats; Party 5: 9 seats; Party 6: 8 seats; Party 7: 6 seats; Party 8: 3 seats; Party 9: 2 seats; Party 10: 1 seat; Party 11: 9 seats; Party 12: 8 seats; Party 13: 6 seats; Party 14: 3 seats; Party 15: 2 seats; Party 16: 1. ENP = 5.77. Here it is possible to observe that the number of parties has less influence. The bigger influence and meaning for the ENP is the relative size between the parties and the power they have, which is seen through the seats of the parties in the legislative house which is, in the end, a relative measure.

4: Linear Deviation Indices

These are indices that use the absolute difference between the proportion of votes of each party and the proportion of seats won by them in the legislative house.

4.1: RAE Electoral System Disproportionality Index

Proposition: Like the previously presented index, the RAE^D was created in 1967 and proposed by Rae (Douglas Whiting Rae; Political Scientist – United States). The RAE^D index measures the disproportionality of party representation in an electoral system. It can be given in numerical form or percentage form. The most common is the first way, although the second is more intuitive.

Equation: The equation that calculates the RAE^D index is presented in equation 4.

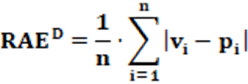
Concepts: Conceptually, the RAE^D index measures the average deviation (and not the total deviation) in an election and verifies the level of disproportionality regarding the number of seats won by the parties concerning the proportion of votes received. It is the oldest index of disproportionality in the electoral system.

From the equation, it’s possible to note that the RAE^D index is average since the sum is divided by the number of parties. Therefore, it measures the average deviation. However, the equation has the problem of duplication of values. To understand this we have to understand the difference between v_i – p_i. The parameter p_i indicates the proportion of seats won by any party. Already v_i is the proportion of votes this party obtained in the elections.

So, when v_i < p_i this means that there was a higher proportion of votes than the proportion of seats won. And as the calculation is based on (relative) proportions, the seats of the party that didn’t win go to another party. Therefore, for party A; v_i – p_i =X; for a party B, we will have v_i – p_i = -X. However, as the value is given in modules, the -X value becomes X; which causes the X value to appear twice; i.e. 2X. That’s why there is a duplicity of values.

This does not mean that the index does not have its value, as this must be considered in the analysis. Furthermore, there is an index that eliminates this duplication of values, as we will see in this article. What we have to understand is that the RAE^D index is an average of the deviation between the proportion of seats won (v_i) and the proportion of votes obtained (p_i). In this way, it allows measuring the level of disproportionality of a given electoral system.

Something we must understand is that within an election when a small party receives the vote (v_i > 0), but does not receive seats (p_i = 0) then the RAE^D index is underestimated. Thus, small parties, with little voting and few or no seats won, underestimate the RAE^D index. One of the elements that contributes to this is the number of parties (n), which goes from n (without the presence of the small party) to n + 1 (with the presence of the small party).

Interpretation: In terms of presentation, it’s suggestive value in percentage form. The idea of ​​interpretation is simple. The lower the calculated value, the less disproportionate the electoral system. For higher values, the greater the disproportionality of the electoral system.

Input data: To calculate the RAE^D index two pieces of data are needed: The first data is the number of votes of the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. By these values, ​​the RAE^D index is determined.

Example: From Table 2, we have Σ| v_i – p_i | = 0.33757; then RAE^D = 33,75%.

4.2: Loosemore–Hanby Electoral System Disproportionality Index

Proposition: The Losemore-Hanby (LH) index was created in 1971, and proposed by Loosemore (John Loosemore) and Hanby (Victor J. Hanby). The LH index measures the disproportionality of party representation in an electoral system.

Proposition: The Losemore-Hanby (LH) index was created in 1971, and proposed by Loosemore (John Loosemore) and Hanby (Victor J. Hanby). The LH index measures the disproportionality of party representation in an electoral system.

Its value can be presented in numerical form when calculated from proportions, or it can be presented in percentage form when calculated from percentage values. Both are used, however, the percentage value is more common.

Equation: The equation that calculates the LH index is presented in equation 5 and is very similar to the equation for the RAE^D index.

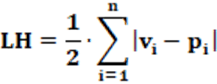
Concepts: Conceptually, the LH index measures the total deviation (and not the average deviation) in an election and verifies the level of disproportionality regarding the number of seats won by the parties concerning the proportion of votes received. It is considered a more real index for analyzing the disproportionality of the electoral system than the RAE^D index. This is due to the total deviation measurement and not the average usage.

It is calculated through the absolute difference, in modules, between the proportion (or percentage) of seats won by that party in the legislative house – (v_i) and the proportion (or percentage) of votes received by a party (p_i). Thus, based on this reasoning, the LH index makes it possible to measure how much an election deviates from the electoral principle: “One person, one vote”. In other words, the LH index informs about the votes wasted.

This is because if you v_i = p_i Thus all votes cast by voters were converted into seats in the legislative house. If v_i > p_i this means that the proportion of votes received was greater than the proportion of seats won by that party. Soon; the difference between v_i – p_i represents the share of voters’ votes for that party that had no relevance in winning seats in the legislative house. In this case, there is harm to the party.

With v_i < p_i this means that the proportion of votes received was lower than the proportion of seats won by that party. Even though for this party the gain of seats was better than its vote, this brings harm to another party because the calculation is made based on proportion, which considers the total value. Therefore; for the latter case, the difference v_i – p_i represents the share of votes of voters who did not vote for that party and nevertheless guaranteed that party the victory of seats in the legislative house. In this case, there is benefit to the party.

Therefore; for every loss to one party there is a benefit to another party. This is because the calculation considers the proportions of seats won by each party (v_i). Given this reasoning, it is possible to note that the result v_i – p_i will appear twice; one in the form of a loss to party A and another time in the form of a benefit to party B. Therefore, to avoid duplication of the same values ​​there is division by 2. It is important to highlight that the calculation uses the module of the difference between the values. Thus, division by 2 prevents the analysis of the same value twice.

Finally, returning to the previous idea, the LH index, as calculated by definition, indicates the number of wasted votes. This is seen when v_i < p_i. Therefore, the LH index measures the disproportionality of an electoral system in a given election. We talk about disproportionality, not proportionality given its formal and mathematical concept.

Interpretation: In terms of presentation, it’s suggestive value in percentage form. The idea of ​​interpretation is simple. The lower the calculated value, the less disproportionate the electoral system. For higher values, the greater the disproportionality of the electoral system.

Input data: To calculate the LH index two pieces of data are needed: The first data is the number of votes by the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i is calculated v_i e p_i, respectively. Using these values, the LH index is determined.

Example: From Table 2, we have Σ| v_i – p_i | = 0.33757; LH logo = 16.87%.

4.3: Rose Electoral System Proportionality Index

Proposition: The ROSE index (RO) was created in 1984, and proposed by Rose (Richard Rose; Political Scientist – United States). The index measures the level of proportional representation of parties in an electoral system in a given country. The numerical value is presented as an index, with values ​​between 0 and 1, but is generally shown in percentage form.

Equation: The equation that calculates the RO index is presented in equation 6.

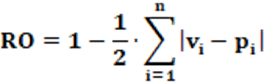
It can also be expressed according to equation 7.

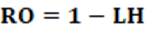
Concepts: Conceptually, the RO index is complementary to the LH index. The Rose index measures the degree of representation of parties within an electoral system in a country. As LH measures the disproportionality of party representation in the electoral system, when this result is subtracted from 1, we obtain the complementary opposite, which is the proportionality of party representation in the electoral system. Disproportionality is seen by the deviation, given by the sum of the difference between v_i e p_i. Once disproportionality is removed, what remains is proportionality. In other words, the proportionality of party representation within the electoral system.

Interpretation: The interpretation of values ​​is straightforward. For high values ​​of the RO index, there is high proportionality in the representation of political parties in the electoral system. Low values ​​of the RO index, indicate low proportionality in the representation of political parties in the electoral system.

Input data: To calculate the RO index two pieces of data are needed: The first data is the number of votes by the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. Using these values, the LH index is determined. We can also use the LH index itself as input data.

Example: From Table 2, we have Σ| v_i – p_i | = 0,33757; logo RO = 83,13%.

4.4: Grofman Electoral System Disproportionality Index

Proposition: The Grofman index (G) was proposed in 1985, by Grofman (Bernard Norman Grofman; Political Scientist – United States). The index is also known as the adjusted Loosemore-Hanby index. The G index measures the disproportionality of party representation in an electoral system.

Equation: The equation that calculates the G index is presented in equation 8.

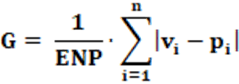
We can observe that ENP = 1/(pi)2. After algebraic manipulations, we will have, as a result, equation 9.

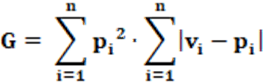
The two equations are, in the end, the same, what changes is their presentation.

Concepts: Conceptually, the G index is the RAE^D and LH index mathematically modified. Regarding the LH index, the G index replaces division by 2 with division by ENP. While the LH index, mathematically, uses and measures the total deviation, the G index measures the same deviation weighted by the ENP; that is a measure of reality regarding the effective number of parties, or, indirectly, party fragmentation.

This results in an important observation. The RAE^D index is calculated from the average deviation since the deviation is divided by the number of existing parties. This is the difference regarding the G index since it is divided by the effective number of parties not by the real number of them. All this implies that the G index has an intermediate value between the RAE^D and LH index. It is an index that uses the deviation between p_i and v_i. values. Because it is a deviation, the value is absolute. What changes, in this case, is the weighting, it’s done through the ENP. As the LH index is weighted by 2 and the RAE^D index has N weighting (number of parties), from this we can say that 2 < ENP < N; which necessarily results in the following relationship: RAE^D < G < LH.

The fact of using ENP as weighting brings a more realistic view. The use of N (in the case of the RAE^D index the use of 2 (in the case of the LH index) as weighting elements is not as realistic as the G index. This is because the ENP reflects the strength of the parties and this strength weights the deviation of the party representation of the parties with significant representation, or, in other words, parties with political relevance and strength.

Thus, the G index has a more realistic character than the RAE^D and LH index because the G index weights its deviation value using a real value measure which is the ENP. An interesting observation is that the RAE^D and the G index can present different values ​​for the same deviations because the denominators vary depending on the case, respectively N and ENP. In the case of the LH index, with the same deviations, the value will always be the same, because the denominator is the same (2), remembering that it is calculated based on the total deviation.

Finally, the G index has the absolute deviation divided equally between all effective parties on the political scene. Therefore, it has a more realistic character. The final value indicates the level absolute of disproportionality |(v_i – p_i)| concerning how much this affects the effective parties (ENP), a way of distributing disproportionality to effective parties.

Interpretation: The interpretation of values ​​is straightforward. For low values ​​of the G index, there is low disproportionality in the representation of political parties in the electoral system. With high values ​​of the G index, there is high disproportionality in the representation of political parties in the electoral system.

Input data: To calculate the G index two pieces of data are needed: The first data is the number of votes of the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. Using these values, the G index is determined.

Example: From Table 2, we have Σ| v_i – p_i | = 0.33757; and ENP = 5.38; therefore G = 6.27%.

5: Quadratic Deviation Indices

These are indices that use the absolute difference between the proportion of votes of each party and the proportion of seats won by them in the legislative house. The difference is squared.

5.1: Gallagher Electoral System Disproportionality Index

Proposition: The Gallagher index (LSq) was created in 1989, and publicly presented in 1991. It was proposed by Gallagher (Michael Gallagher; Political Scientist – United Kingdom). The index measures the disproportionality of party representation in an electoral system in a given country. The numerical value is in the form of an index, with values ​​between 0 and 100.

Equation: The equation that calculates the LSq index is presented in equation 10.

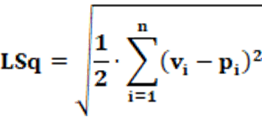
Proposition: The Gallagher index (LSq) was created in 1989, and publicly presented in 1991. It was proposed by Gallagher (Michael Gallagher; Political Scientist – United Kingdom). The index measures the disproportionality of party representation in an electoral system in a given country. The numerical value is in the form of an index, with values ​​between 0 and 100.

Equation: The equation that calculates the LSq index is presented in equation 10.

Concepts: The Gallagher index is a reference used for comparison between countries and is represented as LSq because it alludes to the term Least Square. However, from a mathematical point of view, the name is inappropriate, since there is no minimization of squares. The use of LSq to represent the index is done for reasons of already widespread recognition not for conceptual reasons. Therefore, sometimes, some authors instead of using LSq use “G” to indicate the index. Conceptually, the LSq index starts from the sum of squared residuals. Residual, conceptually, is the difference between an ideal value and an actual or predicted value.

So, v_i represents the ideal value and p_i the real value. The difference between v_i e p_i is the residue. This difference is made for each party i. The residue is squared because if in a given party A v_i – p_i = X, for party B v_i – p_i = -X. This is because the calculation considers the proportions of votes (v_i) and proportions of seats obtained in the legislative house (p_i). Therefore, if party A has a positive variation, resulting in X; this must be compensated, causing party B to have, as a result, -X.

Therefore; if the calculation is not made from the module or it isn’t squared (or another even exponent), the result of the sum will be zero. Therefore, without using the module, one way to ensure that the sum does not result in zero is to use an even exponent, in this case, 2; that is, use of the square. Therefore, the calculation is made, by concept, from the sum of the squares of the residues. The square root is used to return to the original dimension, transforming the squared residue into just a residue. The division by 2 changes the scale of the LSq index, adjusting so that the result is faithful to the data.

For example. Assuming a case of two parties, A and B; party A has 100% of the votes and party B has 0%. Due to some political maneuver, party A is left without any seats in the legislative house and party B wins them all. In this situation, for party A, the residue is 100 – 0; which results in 100. For party B, the residual is 0 – 100; which results in -100. Squaring each of these values, we obtain 10,000; for party A and party B. The sum; therefore, results in 20,000, which when divided by 2, returns to the value 10,000; whose square root is 100. Therefore, the disproportionality of party representation in this electoral system is 100%.

Therefore, if there were no division by 2, the result would be 70.71%. Logically, this value does not match the data in our example. Therefore; division by 2 is a correct calculation. We must remember that the calculation when we deal with the difference between proportions, always occurs twice. Therefore, division by 2 is not the result of chance. In terms of sensitivity, small changes, caused by small parties, are what are most sensitive. Therefore, it gives a good reading regarding the disproportionality of party representation in a given electoral system.

Interpretation: Although the index is commonly presented as a numerical value, it can easily be interpreted as if it were a percentage. This occurs because the index has values ​​between 0 and 100. For an index of 0, we have the ideal case of representation, without any disproportionality of party representation in the electoral system. In the case of an index of 100, this represents the greatest distortion, that is, the greatest disproportionality of party representation in the electoral system. For values ​​between 0 and 100; the interpretation is straightforward. The higher the index, the greater the disproportionality of party representation in the electoral system.

Input data: To calculate the LSq index two pieces of data are needed: The first data is the number of votes of the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. Using these values, the LSq index is determined.

Example: From Table 2, we have Σ| v_i – p_i |² = 0,03770; logo LSq = 13,72%.

5.2: Sainte-Lagüe Index of Electoral System Disproportionality

Proposition: The Sainte-Lagüe index (SL) is based on studies by French mathematician André Sainte-Lagüe. It was created by Gallagher, the same as the Gallagher – LSq index. The index measures the disproportionality of party representation in an electoral system in a given country. The numerical value is in percentage form, as well as the values ​​used for the calculation, which instead of proportional values, previously used, uses values ​​already in percentage form.

Equation: The equation that calculates the SL index is presented in equation 11.

Concepts: The Sanite-Lagüe index has the format of the Chi-Square probability distribution. In this format, we have, the difference between the observed value O_i; and the expected value E_i. This difference is squared and divided by the expected value, E_i. In our case, P_i% and V_i% are equivalent to O_i and E_i, respectively.

The equation presents the sum of squared residuals, similar to the LSq index. However, instead of dividing by 2 and extracting the root, to return to the same dimension; weighting is performed, which is division by V_i%. This weighting allows the distribution of the value of the residuals for each of the votes received by the party i. Represents the weight that each party has in voting (V_i) in the total vote V. That is, the SL index calculates the proportion of votes lost (which were not converted into seats in the legislative house) or of votes gained in addition to its vote (seats in the legislative house won without the corresponding vote) distributed for each voter, which is the expected value, according to the electoral principle “One person, one vote”, as described in the LH index.

In short, the SL index measures the dispersion of residuals (difference between expected and real) for the universe of voters voting for the party i. Expected and actual are understood, respectively, as V_i% e P_i%. The Chi-Square test, as the SL index, aims to compare proportions (in our case V_i% e P_i%) and estimate the divergence between the expected value V_i% and the real value P_i%.

As the SL index is divided by V_i%; this represents that the highest votes V_i present greater dispersion of the square of residuals (or relative deviation) per voter; minimizing the SL index. In the case of V_i having low values, the opposite occurs, that is, the dispersion of relative deviations, per voter, is maximized; increasing the SL index. Of course, the deviation value must also be considered, mainly because it is squared. Therefore, the absolute difference between V_i% and P_i% strongly influences the index. But even so, even with high values ​​of relative deviation (residuals), the quotient is capable of minimizing disproportionality. Therefore, we have a balance seen exactly through the weighting, given by the SL index quotient.

Finally, for possible results, we should not use parties with no votes or be parties with V_i = 0. This is because 1/V_i goes to infinity and that takes SL to infinity. If the limit is applied at this point, it turns out that it does not exist because the values ​​on the left and right sides are different, which makes the limit non-existent, according to equation 12 and the resolution below.

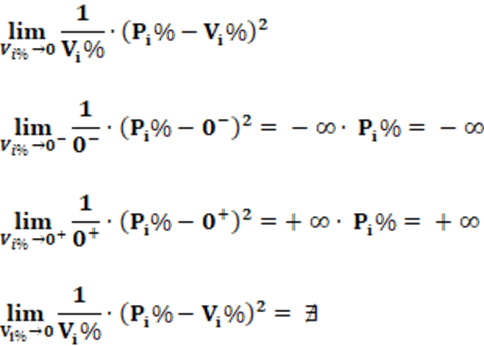
Interpretation: The interpretation of the SL index is straightforward and given in percentage terms. For low values, we have less disproportionality of party representation in the electoral system. For high values ​​of the SL index, the disproportionality of party representation in the electoral system is equally high. SL index values ​​range from 0 to infinity; which incurs apparent incongruity that only occurs in an extreme case. Values ​​above 100 are quite common. The infinite value appears when any party, without any vote (V_i = 0); wins a seat. This makes 1/V_i go to infinity because in this case V_i = 0.

Input data: To calculate the SL index two pieces of data are needed: The first data is the number of votes obtained by each party, in percentage terms (V_i%). The second necessary data is the number of seats by the party in percentage terms (P_i%). Thus, from V_i% e P_i% the SL index is calculated.

Example: From Table 3 we have the direct value of the SL index; since SL = Σ( | V_i%- P_i% |²/IN_i%)= 2,1724; logo SL = 217,24%.

5.3: Monroe Electoral System Disproportionality Index

Proposition: The Monroe Index (MO) was created in 1994. It was proposed by Monroe (Burt L. Monroe; Professor of Political Science – United States). The index measures the disproportionality of party representation in an electoral system in a given country. The numerical value is in the form of an index, with values ​​between 0 and 100.

Equation: The equation that calculates the MO index is presented in equation 13.

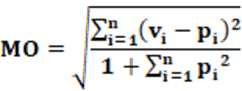
Concepts: Conceptually, the MO index starts from the sum of squared residuals. As seen in the LSq index, the residual is, conceptually, the difference between an ideal value and an actual or predicted value. In the case of the Lsq index, the denominator is “2”. In the case of the MO index, the denominator is “1 + Σ(p_i)²“. For analysis purposes, it is convenient to carry out some algebraic manipulations. The first thing to do is consider that Σ(p_i)² = 1/ENP. After this substitution and some algebraic manipulations, equation 13 is transformed into equation 14.

This results in the MO index changing according to each situation, as the ENP value in each case is different. This gives an advantage concerning the LSq index since this last index does not change depending on the case because the denominator is fixed, in this case, 2. On the contrary, the MO index has a correction in each case since it is used to correct the ENP. It is possible to observe that the correction factor (ENP/(ENP+1)) will always result in a value less than 1, that is, (ENP/(ENP+1)) < 1 because the numerator is smaller than the denominator.

Other algebraic manipulations allow estimating the MO index from the LSq index. Equation 15 shows this relationship.

Except for the correction factor, every concept for the LSq index is also valid for the MO index. Therefore; the idea remains. An interesting observation is that for the particular case of ENP = 1; the value of the MO index is the same as the LSq index. A second observation is that for any ENP value other than 1, the MO index will always be greater than the LSq index. This occurs because the multiplicative factor for the LSq index is 0.5 (= 1/2) and the MO index, will be greater than 0.5, in the case of ENP > 1. Furthermore, the higher the ENP, the greater the factor correction factor (multiplicative factor), so when ENP → ∞ the correction factor will tend to be 1.

Finally, equation 15 can be rewritten according to equation 16.

Interpretation: The index is presented as a numerical value. For greater values of the index, the distortion will be bigger, and as a consequence, there will be greater disproportionality of party representation in the electoral system. In smaller values ​​of the index, the idea is the same, the disproportionality of party representation in the electoral system will be lower. Therefore, like most indices, interpretation is straightforward. Finally, equation 16 shows, mathematically, that for ENP > 1; the MO index will always be greater than the LSq index.

Input data: To calculate the MO index two pieces of data are needed: The first data is the number of votes of the party (V_i). The second necessary data is the number of seats by the party (P_i). Thus, from V_i e P_i v is calculated_i e p_i, respectively. By these values, ​​the MO index is determined.

Example: From Table 2, we have Σ| v_i – p_i |² = 0.03770; and with ENP = 5.38; using equation 14, we have MO = 17.83%.

6: Overrepresented Indices

These are indices that consider the largest absolute difference between the proportion of votes of each party and the proportion of seats won by them in the legislative house.

6.1: Maximum Deviation Index of Disproportionality of the Electoral System

Proposition: The Maximum Deviation (MD) index is cited in one of Lijphart’s works in 1994. The index measures the disproportionality of party representation in an electoral system in a given country based on the absolute difference (and not relative) between the proportion of seats obtained by a party and the proportion of votes of that same party. The choice of party is on the value that provides the greatest difference between p_i and v_i.

Equation: The equation that calculates the MD index is presented in equation 17.

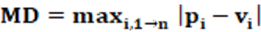
Concepts: The MD index characterizes the disproportionality of party representation in the electoral system through the highest disproportionality value. Thus, he uses the largest absolute difference between the proportion of the number of seats in the legislative house (p_i) and the proportion of the number of votes that the party received (v_i). The measure is simple to obtain, quick to calculate, and allows a reasonable view of the disproportionality of the electoral system. It is important to note that the largest difference between the proportion p_i and v_i, will not necessarily be from the largest party. It’s possible to happen being quick common that the biggest difference occurs for the second or third largest party. Therefore, it must be clear that it is not a question of using data from the bigger party, but of considering the values ​​of the party with the greatest absolute difference between p_i and v_i.

Interpretation: The interpretation of the MD index occurs with direct reading. For small values, the disproportionality of party representation is low. If the values ​​are high, the disproportionality of party representation is high. The values ​​range from 0 to 1. It will be 1 when a party that did not receive any votes won all the seats.

Input data: To calculate the MD index two pieces of data are needed: The first data is the number of votes of the party (v_i). The second necessary data is the number of seats by the party in percentage terms (p_i). By comparing the difference between all the values ​​obtained for each party, thus the MD index is determined.

Example: From Table 2, we have that the largest absolute value |v_i-p_i|, corresponds to party 3 and is worth 0.18222; which makes MD = 18.22%.

6.2: Lijphart Index of Electoral System Disproportionality

Proposition: The Lijphart Index (LJ) was created in 1994, and proposed by Lijphart (Arend D’Engremont Lijphart; Political Scientist – Netherlands). The index measures the disproportionality of party representation in an electoral system. The index value is given in numerical form, not in percentage form.

Equation: The equation that calculates the LJ index is presented in equation 18.

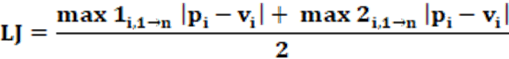
Concepts: The Lijiphart index (LJ) characterizes the disproportionality of party representation in the electoral system and is calculated by the arithmetic mean of the two values ​​with the greatest disproportionality. This is calculated by subtraction between the absolute difference in the proportion of the number of seats in the legislative house (p_i) and the proportion of the number of votes that the party received (v_i). The value calculated, like the previous index, is simple to obtain, quick to calculate, and allows a reasonable view of the existing disproportionality. Vision is sharper than the previous MD index. It is also important to note that the two biggest differences between the proportion p_i and v_i, will not necessarily be from the two largest parties. The values must be guided by the greatest differences and not concerning the size of the parties, that is, the number of votes received or the number of seats won.

An interesting analysis is that the LJ index is a particular case of the RAE^D index disproportionality. Instead of “n” as a quotient, “2” is used. The quotient proportion is the same because, in the RAE^D index the arithmetic average is, for “n” elements, so this is the denominator. In the case of the LJ index, as the average is made from two elements the denominator is “2”. The idea is the same, what changes is the number of elements used.

Interpretation: The interpretation of the LJ index occurs, like the previous index, with direct reading. For small values, the disproportionality of party representation is low. If the values ​​are high, the disproportionality of party representation is high. Values ​​range from 0 to 1.

Input data: To calculate the LJ index two pieces of data are needed: The first data is the number of votes of the party (v_i). The second necessary data is the number of seats by the party in percentage terms (p_i). By comparing all the values ​​obtained for the parties, thus is determined the LJ index.

Example: From Table 2, we have that the largest absolute value |v_i-p_i|, corresponds to party 3 and is worth 0.18222; the second largest absolute value |v_i-p_i|, corresponds to party 6 and is worth 0.05294; which makes LJ = 0.1175, or, in (non-conventional) percentage form, 11.75%.

6.3: D’Hont Index of Electoral System Disproportionality

Proposition: The D’Hont index is based on D’Hont’s studies (Victor Joseph Auguste D’Hondt; Civil law lawyer – Belgium). The index measures the disproportionality of party representation in an electoral system. The idea of ​​the index is to maintain the lowest possible value for the overrepresentation of the most overrepresented party.

Equation: The equation that calculates the DH index is presented in equation 19.

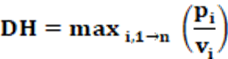
Concepts: The D’Hondt index (DH) indicates the disproportionality of party representation through the quotient between the proportion of the number of seats in the legislative house (p_i) and the proportion of the number of votes that the party received (v_i) from the most overrepresented party; that is, what happens when |(p_i – v_i)| = max< |(p_i – v_i)| >. Therefore, even if the Maximum Deviation (MD) index is not calculated it’s necessary to indicate which party has the greatest overrepresentation. In general, this happens with larger parties. However, if overrepresentation occurs with smaller parties, the index has an unrealistic analysis because it results in an index with a higher value than it is.

The D’Hondt index measures the discrepancy in the values ​​of the most overrepresented party. Therefore, to calculate the D’Hondt index we must always have p_i > v_i. Therefore, under these conditions p_i/v_i; > 1. In an ideal case, p_i = v_i, we will have p_i/v_i; = 1. Thus, the existence range of the D’Hondt index is from 1 to infinity. Value 1 is for an ideal case. The infinite value is when a party that did not receive any votes won at least one seat in the legislative house. When v_i = 0; what then does p_i/v_i go to infinity. In this case, the index is anomalous value and in the case of an overrepresentation of a small party, the value is unrealistic.

Even so, even with these exceptions, overall, the D’Hont index has a good indication. The only thing that needs attention is the exceptional cases of overrepresentation with small parties. A solution that can be applied in these cases is to impose a cutoff line of 5 to 10% from the values p_i and v_i; depending on the case or method to be applied and understood by the analyst. The great advantage of the DH index is its ease of calculation and the good indication of disproportionality in general cases, which does not include exceptional cases. Furthermore, it keeps the overrepresentation of the most overrepresented party to a minimum, not creating high values ​​that can alter reality when an analysis is carried out.

Interpretation: The interpretation of the DH index occurs from a direct reading of the index. Values ​​close to 1 result in low disproportionality of party representation in the party system. The further away from 1, the greater the disproportionality. Values ​​above 1,000 or 2,000 are common for this index in the case of high disproportionality in the electoral system.

Input data: To calculate the DH index two pieces of data are needed: The first data is the proportion of votes obtained by each party (v_i). The second necessary data is the proportion of seats by the party (p_i). Comparing all the values ​​obtained for the parties thus we determined the DH index.

Example: From Table 2, we have that the largest absolute value |v_i-p_i| corresponds to party 3 and is worth 0.18222; then, v_i = 0,2040 e p_i = 0.2222; or that results in no value of DH = 1.089.

7: Measures of Surplus Values

These are indices that consider votes that are not used in an election for reasons of technical origin.

7.1: Wasted Vote

Proposition: The Wasted Vote was proposed in 2015 by Stephanopoulos (Nicholas Stephanopoulos; Lawyer – United States) and McGhee (Eric McGhee; Political Scientist – United States). It is not the main idea, just part of an idea that allows the Efficiency Gap to be calculated.

Equation: The equation that calculates the W index is presented in equation 20.

Concepts: Conceptually, Wasted Vote (W) is every vote that does not generate representation. From this premise, two types of wasted votes arise. The excess vote (V⁺) is the number of votes that exceed the value necessary for the party or candidate to win the seat in the legislative house. There is still the lost vote (V^–) which is the vote given to the party or candidate that did not win the seat in the legislative house. The sum of these votes is the wasted vote. Therefore; From the relationship between the number of wasted votes and the number of total votes, a relationship is obtained that, presented in percentage form, represents the wasted vote. This way it is possible to measure the number of votes converted into representation and how many votes were wasted.

Interpretation: The interpretation of the W index is straightforward. The higher the percentage, the greater the number of wasted votes. Average values ​​are around 50%.

Input data: To calculate the W index, it is only necessary to know the votes of each party or candidate, as the case may be, and from this, it is possible to calculate the total number of votes and select the excess votes (V⁺) and lost votes (V^–). Using these data, the W index is calculated.

Example 1: Consider the data in Table 4, election 1 for a majority election. As the election is of type majority, candidate A wins the seat and all other candidates lose their votes. Thus, the value of (V^–) considers the votes of candidates B, C, D, and E; which results in 39,900,000 votes; i.e. V^– = 39,900,000. Regarding candidate A; he would have won the seat with 31,000,001 votes; therefore, the difference between this and 60,000,000 is A’s excess votes, that is; V⁺ = 28,999,999 votes. The total number of votes in this election is 100,000,000; This results in the number of wasted votes W, which is worth 68,899,999 (= 39,900,000 + 28,999,999); which results in 68.89%.

Example 2: Consider the data in Table 4, election 2 for a proportional election of 2 seats, with distribution based on the D’Hont method. For candidate A; using the D’Hont method, considering 2 chairs, we have the sequence: 60,000,000, 30,000,000, 15,000,000. For candidate B, we have 31,000,000, 15,500,000, and 7,750,000. For candidate C, we have 7,000,000, 3,500,000, and 1,750,000. Thus, the first seat is obtained by candidate A, for the amount of 60,000,000 in the first round of seat distribution and the second seat is obtained by candidate B for the amount of 31,000,000. Therefore; candidate C did not obtain a seat. Thus, the number of lost votes is the number of votes for candidate C, that is, V^– = 7,000,000 votes. Now we must calculate the excess votes of A and B. For A, we have 60,000,000/7,000,000, which results in 8.57. Using the unit, we have 8, multiplied by 7,000,000 and added by 1 resulting in 56,000,001 votes. This value subtracted from 60,000,000 is candidate A’s excess votes, resulting in 3,999,999. The same result can be obtained as follows; 8.57 – 8 = 0.57. This value multiplied by 7,000,000, results in 3,999,999.9998. Using the entire portion, we have the same 3,999,999. For candidate B, the excess votes follow the same idea, 31,000,000/7,000,000, which results in 4.42, which when using the entire part, results in 4, multiplied by 7,000,000 and added by 1, results in 28,000. 001 votes. This value subtracted from 31,000,000 results in B’s excess votes and is worth 2,999,999 votes. Thus, from the sum of the excess votes of A and B, we have V⁺ = 6,999,998. Therefore, the value W, for this case, is worth 13,999,998 ( = 7,000,000+ 6,999,998); which results in 14.28%.

7.2: Efficiency Gap

Proposition: Also proposed by Stephanopoulos (Nicholas Stephanopoulos; Lawyer – United States) and McGhee (Eric McGhee; Political Scientist – United States), in 2015. This is the main idea, which requires the values ​​of Wasted Votes (W) to be calculated. The index is generally given in percentage form. Too can be shown in numerical form (proportion). It indicates how fair a district election is and, by inference, how much manipulation allowed the results of an election to be modified if it were held fairly. It is used for two-party systems with the application of gerrymandering analysis.

Equation: The equation that calculates the GAP index is presented in equation 21.

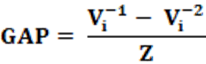
Concepts: The GAP analysis makes it possible to identify the wasted votes of each party, especially the two largest parties, and analyzes whether one of them had an advantage in converting votes to seats in the legislative house. With preferable use for the district vote, the GAP makes it possible to identify which party benefited and which suffered harm. The index was, temporarily, recently constructed, and few studies about it, its efficiency, and its results. For construction and interpretation purposes, it is interesting to maintain how (V_i)^-1 is the party that received the highest total vote and (V_i)^-2 is the party that received the second highest vote. Thus, the interpretation now has a constant for analysis.

Interpretation: The interpretation of the GAP index is straightforward, however it is necessary to evaluate the GAP signal. Based on the indicated construction when the GAP is positive, the election benefited the party with the second highest vote. Case the value is negative, the election benefited the party with the highest votes. Regardless of the sign, the absolute value directly indicates the size of the distortion and, how fair the election is, or even how far it is from an election considered fair.

Input data: To calculate the GAP, only one piece of data is needed, and that is the number of votes obtained by each party, in percentage terms (V_i%). From this universe, the total votes and the votes of the two largest parties are used.

Example 1: From the data in Table 4, considering that instead of candidates we have parties, and the calculations already carried out in the previous item, we have, for election 1, (V_i)^-1 = 28,999,999 e (V_i)^-2 = 31,000,000; with a vote of 100,000,000 votes, we have GAP = 59.99%.

Example 2: From the data in Table 4, considering that instead of candidates we have parties, and the calculations already carried out in the previous item, we have, for election 2, (V_i)^-1 = 3,999,999 e (V_i)^-2 = 2,999,999; with a vote of 98,000,000 votes, we have GAP = 7.14%.

8: Electoral Mobility Indexes

These indices measure the movement of parties and their stability in the electoral and party system, which takes into account variations over the timeline.

8.1: Pedersen Electoral Volatility Index

Proposition: The Pedersen (P) index was created in 1979 by Pedersen (Mogens Jin Pedersen; Political Scientist – Denmark). The index measures electoral volatility, it indicates the net change that occurs in the electoral system from an election t-1 to an election t. This is seen in the temporal change of the elector’s vote, a change called individual vote transfer. Global change is the sum of all individual change.

Equation: The equation that calculates the P index is presented in equation 22.

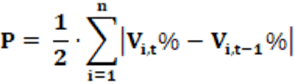
Concepts: The P index has mathematically, the same format as the LH index. In other words, it is calculated from the total deviation. It considers absolute values ​​and, therefore, consequently, a percentage X lost between two elections by party A, the same value percentage will be gained by party B. This results in |Vi,t% – INi,t-1%| will appear twice, once as -X (part A) and once as +X (part B). As they are absolute values, the two values ​​enter the sum as X, which results in 2X. As there is division by 2; At the end, the resulting value will be X.

Therefore, the entire mathematical conceptual idea of ​​the LH index can be applied to the P index. The difference between the indices lies in their ideological construction. The P index uses the difference in votes, in percentage form, between two elections, not necessarily in consecutive elections. Thus, the P index measures the change in votes that voters impose on parties between two elections. Many inferences can be made from this index, especially if the transfer of votes between parties is evaluated, considering who won and who lost, and even more so, how much was gained and lost. This way it is possible to measure voter satisfaction and dissatisfaction. Thus, electoral volatility indicates the mobilization of voter intention and prints this in percentage form.

Interpretation: The interpretation of the P index is straightforward, through the percentage value of the index itself. The higher the percentage value, the greater the changes, or, in technical terms, the greater the transfer of votes. In this case, there is an indication of a significant alteration in political representation. Low values ​​indicate lower vote transfers. In this case, there was no significant change, in the representation. Finally, the level of contentment or discontent, inferred by the P index, suggests the level of political instability in a given country. Discontent is seen by the attempt to change, which indicates a high P index. Societies satisfied with their representation do not find meaning in changing their representation; which results in a low P index.

Input data: To calculate the P index, only one piece of data is needed, and it is the number of votes obtained by each party, in percentage terms (Vi%). However, this value is obtained at two different times not necessarily in consecutive elections. Thus, from Vi,t% is Vi, t-1% the index P is calculated.

Example: From Table 5, we can calculate the P index for various moments. Let’s calculate the P index between elections 9 (year 2016) and 10 (year 2020). Thus, the percentage difference for each party is: Party A = 3.6%; Party B = 8%; Party C = 2.6%; Party D = 1.2%; Party E = 0.6%. Thus, between the 2020/2026 elections, the P index = 8%.

8.2: Lewis Party Stabilization Index

Proposition: The Lewis Index of Party Stabilization (LW) was created in 1994 by Lewis (Paul G. Lewis; Political Scientist). The index measures the stability of parties in the political scenario, based on their permanence in the political arena over the timeline.

Proposition: The Lewis Index of Party Stabilization (LW) was created in 1994 by Lewis (Paul G. Lewis; Political Scientist). The index measures the stability of parties in the political scenario, based on their permanence in the political arena over the timeline.

Concepts: The LW index measures the electoral success of each party over a timeline considering the results of several elections. The longer a party remains on the political scene, the greater its success, which is done by applying weights (rewards) to the relative proportion of votes obtained. These weights (rewards) increase with each new election. Therefore, the maintenance of a party represents the stabilization of that party and we consider the stabilization of all parties, we have the partisan stabilization of the electoral system, a global reading. The LW index is calculated for each election and changes depending on the election. Thus, along the timeline, it is possible to obtain a measure of party stabilization within the electoral system.

The calculation is weighted based on the concept of notional score, which is the sum of the weight in percentage form throughout the elections. For the first analysis (first election) in the timeline, the notional score is 100 and the weight is zero. In the second analysis (second election) the weight is worth 20% (0.2) and the notional score is 100% plus 120% (= 100 +20), that is, 220%. In the third analysis (third election) the weight is worth 40% (0.4) and the notional score is worth 220% plus 140% (= 100 + 40), that is, 360%. This way, the current value is weighted by the sum of the notional score of the analyzed histories.

Thus, the weighting is done. Furthermore, the weight is applied depending on the party’s entry into the political arena. For the party’s first participation, the analysis considers that the weight attributed to the party’s vote will always be zero, even if the analysis already exists for previous years. In other words, the weight rewards not only the permanence of the party but also its existence and temporal origin. If the analysis started in year X, and there are two parties (A and B), for this year the weight for both parties is zero. For year X+4; with the entry of a third party (C), the weight for parties A and B will be 0.2 (1.2 in total) and party C will have zero weight. For year X+8; the value is 0.4 (1.4 in total) for parties A and B and a weight of value 0.2 (1.2 in total) for party C.

In this way, weights are assigned to the parties, which affect the percentage proportion of their votes. It is important to highlight that the weights are based on consecutive elections, not depending on the number of years between them. The measure is by election. The LW index measure uses the standard weight of 20%. To calculate the LW index, we must consider, in addition to the notional score, the historical sum of the LW indexes is called the weighted nominal score. The latter must be divided by the first and the result must be multiplied by 100. The result is given in percentage form. An important note is that the notional score and the LW index use historical values ​​to calculate the LW for the year under analysis.

Interpretation: The LW index is read directly. The higher the value and closer to 100, the greater the maintenance of the party system over time. The increase in the index between elections means constancy in the party system, or even that it has not changed, remaining unscathed. If the index decreases, it means changes in the party system.

Input data: To calculate the LW index, the necessary input data is the percentage of votes each party received in each election, within a period (of time).

Example: From the data in Table 5 and the standard weight 20, by election, we have. The first step is to calculate the votes by applying the weights for each party, thus, we have: PARTY A; percentage by-election: election 1 – 51.2%; election 2 – 46.8% x 1.2 = 56.16%; election 3 – 30.4% x 1.4 = 42.56%; election 4 – 27.2% x 1.6 = 43.5.2%; election 5 – 36.2% x 1.8 = 65.16%; election 6 – 29.4% x 2 = 58.8%; election 7 – 15.9% x 2.2 = 34.98%; election 8 – 30.1% x 2.4 = 72.24%; election 9 – 35.6% x 2.6 = 92.56%; election 10 – 32.0% x 2.8 = 89.6%. PARTY B; percentage by election: election 1, – 44.3%; election 2 – 42.4% x 1.2 = 50.88%; election 3 – 42.1% x 1.4 = 58.94%; election 4 – 38.5% x 1.6 = 61.6%; election 5 – 31.7% x 1.8 = 57.06%; election 6 – 32.9% x 2 = 65.8%; election 7 – 36.7% x 2.2 = 80.74%; election 8 – 7.8% x 2.4 = 18.72%; election 9 – 21.5% x 2.6 = 55.9%; election 10 – 29.5% x 2.8 = 82.66%. PARTY C; percentage per election: election 1, – 4.5%; election 2 – 10.8% x 1.2 = 12.96%; election 3 – 27.5% x 1.4 = 38.5%; election 4 – 34.3% x 1.6 = 54.88%; election 5 – 29.2% x 1.8 = 52.56%; election 6 – 33.0% x 2 = 66.0%; election 7 – 42.4% x 2.2 = 93.28%; election 8 – 58.3% x 2.4 = 139.92%; election 9 – 37.8% x 2.6 = 98.28%; election 10 – 35.2% x 2.8 = 98.56%. PARTY D; percentage per election: election 5 – 2.9%; election 6 – 1.8% x 1.2 = 2.16%; election 7 – 1.7% x 1.4 = 2.38%; election 8 – 2.3% x 1.6 = 3.68%; election 9 – 2.3% x 1.8 = 4.14%; election 10 – 1.1% x 2 = 2.2%. PARTY E; percentage per election: election 6 – 2.9%; election 7 – 3.2% x 1.2 = 3.84%; election 8 – 1.5% x 1.4 = 2.1%; election 9 – 2.8% x 1.6 = 4.48%; election 10 – 2.2% x 1.8 = 3.96%. The second step is to add the final percentages for each election considering the history. So we have: Election 1 – 100%; Election 2 – 120% + 100% = 220%; Election 3 – 140% + 220% = 360%; Election 4 – 160% + 360% = 520%; Election 5 – 177.68% + 520% ​​= 697.68%; Election 6 – 195.66 + 697.68% = 893.34%; Election 7 – 215.22% + 893.34% = 1108.56%; Election 8 – 236.66% + 1108.56% = 1345.22%; Election 9 – 255.36% + 1345.22% = 1600.58%; Election 10 – 276.98% + 1600.58% = 1877.56%. The third step is to calculate the notional values, for each election, so we have: Election 1 – 100%; Election 2 – 120% + 100% = 220%; Election 3 – 140% + 220% = 360%; Election 4 – 160% + 360% = 520%; Election 5 – 180% + 520% ​​= 700%; Election 6 – 200% + 700% = 900%; Election 7 – 220% +900% = 1120%; Election 8 – 240% + 1120% = 1360%; Election 9 – 260% + 1360% = 1620%; Election 10 – 280% + 1620% = 1900%. Finally, the last step is the calculation of the LW indices for election, dividing the values ​​from step 2 by the respective values ​​from step 3. Thus we have: Election 1 – LW = 100%; Election 2 – LW = 100%; Election 3 – LW = 100%; Election 4 – LW = 100%; Election 5 – LW = 99.66%; Election 6 – LW = 99.26%; Election 7 – LW = 98.97%; Election 8 – LW = 98.91%; Election 9 – LW = 98.80%; Election 10 – LW = 98.81%. These are the historical values ​​of the LW index from Table 5.

8.3: Established Party Dominance Index

Concepts: The Established Party Dominance Index (EDP) is, conceptually, the same idea as the LW index. However, there is a difference in weight. In the case of the LW index, the 20% weight is assigned according to the elections, without considering the time between them. In the EDP index, the weight value is 5%, and is assigned per year. Thus, depending on the distance in years between each election, this will be the weight. For one year the weight is 5%; for two years it is 10%, and so on. The difference between the LW and the EDP index is that the first considers sequential elections and the second the temporal distance between sequential elections.

The idea of ​​the LW index is to verify the stability of the party system between elections, regardless of how long this occurs. The EDP index checks the stability of the party system between elections considering the time of the occurrence. Except for the attribution of weights, everything else is the same in terms of calculation and too in conceptual terms.

Interpretation: The Established Party Dominance Index (EDP) is read directly. The higher the value, the higher the level of maintenance of the party system on the timeline. If the value increases from one election to another, the maintenance of the party system remains constant. However, if the value decreases between elections, dominance decreases, and this occurs due to the smaller number of votes dedicated to the parties by voters.

Input data: Like the LW index, and the EDP index the input data is the percentage of votes the party received in each election, within a certain period (of time).

Example: From the data in Table 5 and the standard weight 5, per year, we have. The first step is to calculate the votes by applying the weights for each party, thus, we have: PARTY A; percentage by-election: election 1, – 51.2%; election 2 – 46.8% x 1.2 = 56.16%; election 3 – 30.4% x 1.3 = 39.52%; election 4 – 27.2% x 1.45 = 39.44%; election 5 – 36.2% x 1.5 = 54.3%; election 6 – 29.4% x 1.7 = 49.98%; election 7 – 15.9% x 1.8 = 28.62%; election 8 – 30.1% x 1.9 = 57.19%; election 9 – 35.6% x 2.1 = 74.76%; election 10 – 32.0% x 2.3 = 73.6%. PARTY B; percentage by election: election 1, – 44.3%; election 2 – 42.4% x 1.2 = 50.88%; election 3 – 42.1% x 1.3 = 54.73%; election 4 – 38.5% x 1.45 = 55.825%; election 5 – 31.7% x 1.5 = 47.55%; election 6 – 32.9% x 1.7 = 55.93%; election 7 – 36.7% x 1.8 = 66.06%; election 8 – 7.8% x 1.9 = 14.82%; election 9 – 21.5% x 2.1 = 45.15%; election 10 – 29.5% x 2.3 = 67.85%. PARTY C; percentage per election: election 1, – 4.5%; election 2 – 10.8% x 1.2 = 12.96%; election 3 – 27.5% x 1.3 = 35.75%; election 4 – 34.3% x 1.45 = 49.735%; election 5 – 29.2% x 1.5 = 43.8%; election 6 – 33.0% x 1.7 = 56.1%; election 7 – 42.4% x 1.8 = 76.32%; election 8 – 58.3% x 1.9 = 110.77%; election 9 – 37.8% x 2.1 = 79.38%; election 10 – 35.2% x 2.3 = 80.96%. PARTY D; percentage per election: election 5 – 2.9%; election 6 – 1.8% x 1.2 = 2.16%; election 7 – 1.7% x 1.3 = 2.21%; election 8 – 2.3% x 1.4 = 3.22%; election 9 – 2.3% x 1.6 = 3.68%; election 10 – 1.1% x 1.8 = 1.98%. PARTY E; percentage per election: election 6 – 2.9%; election 7 – 3.2% x 1.1 = 3.52%; election 8 – 1.5% x 1.2 = 1.8%; election 9 – 2.8% x 1.4 = 3.92%; election 10 – 2.2% x 1.6 = 3.52%. The second step is to add the final percentages for each election considering the history. So we have: Election 1 – 100%; Election 2 – 120% + 100% = 220%; Election 3 – 130% + 220% = 350%; Election 4 – 145% + 350% = 495%; Election 5 – 148.55% + 495% = 643.55%; Election 6 – 167.07 + 643.55% = 810.62%; Election 7 – 176.73% + 810.62% = 987.35%; Election 8 – 187.8% + 987.35% = 1175.15%; Election 9 – 206.89% + 1175.15% = 1382.04%; Election 10 – 227.91% + 1382.04% = 1609.95%. The third step is to calculate the notional values, for each election, so we have: Election 1 – 100%; Election 2 – 120% + 100% = 220%; Election 3 – 130% + 220% = 350%; Election 4 – 145% + 350% = 495%; Election 5 – 150% + 495% = 645%; Election 6 – 170% + 645% = 815%; Election 7 – 180% + 815% = 995%; Election 8 – 190% + 995% = 1185%; Election 9 – 210% + 1185% = 1395%; Election 10 – 230% + 1395% = 1625%. Finally, the last step is the calculation of the EDP indices for each election, dividing the values ​​from step 2 by the respective values ​​from step 3. Thus we have: Election 1 – EDP = 100%; Election 2 – EDP = 100%; Election 3 – EDP = 100%; Election 4 – EDP = 100%; Election 5 – EDP = 99.77%; Election 6 – EDP = 99.46%; Election 7 – EDP = 98.23%; Election 8 – EDP = 99.16%; Election 9 – EDP = 99.07%; Election 10 – EDP = 99.07%. These are the historical values ​​of the EDP index from Table 5.

8.4: Party Age

Concepts: Party Age or Average Party Lifetime (Tp), isn’t an index, but a value that, based on some assumptions, allows us to indicate the average party age for a given election. For a given party to be able to count its value in the calculation, the following premise must be met: That the party in the given election has received at least 3% of the votes. Parties that have a lower value are not part of the calculation. The value of 3% suggests a cutoff line for the calculation.

Party age, among other things, gives an idea of ​​party mobilization. If the average age is low, it indicates the existence of many newly created parties, which allows us to infer two things. The first is that popular dissatisfaction is high this is reflected in the creation of new parties. The second is that there has been a recent change in the political/electoral system. If the average age is high, it indicates the persistence of the parties over time, that is, that there is a certain organizational order that guarantees the permanence of the parties. In other words, it represents that the parties and their organizational systems, both long-established, have not only persisted but have been replaced by new parties.

The average used for the calculation is the arithmetic mean. When weighted average is used to calculate party age, using the percentage of votes for each party considered as a weighting weight, we will have an idea whether society supports more new ideas, or not, in this case, it remains rooted in the same ideas. In this case, if the party age is low, it indicates that the society does not conform to old ideas and is looking for a solution to new ideas.  The average age can also be calculated by weighting according to the time of existence, which would result in another result, indicating the average age depending on the persistence of the parties.

Example: From Table 5, we have the following chronological ages of the parties, to the year 2024, Party A, 44; B, 42; C, 30; D, 20 and E, 19. However, the criterion requires that the party has reached 3% of votes in some elections, and, in this sense, Party D doesn’t meet this criterion. Therefore, the chronological age of Party D isn’t taken into the calculation. Thus, based on the arithmetic average of the chronological ages of parties A, B, C, and E, we have the party age which results in 33.75 years; or even 33 years and 9 months.

8.5: Party Institutionalization Index

Concepts: This index measures, at the same time, the level of internal organization of the parties and the capacity acquired by them, over time, to move society and its opinions. The measure is not unitary, that is, it is not a measure per party, but the set of them, so the measure is global, therefore, the index is a measurement of the Party System, which is made up of all parties in the political arena.

The calculation uses two parameters, already discussed. The average age of the parties (Tp) which is, in fact, the average age of the group formed by all parties that act in the elections considering a cutoff line based on the votes obtained. This index measures the level of permanence and persistence of a party. In addition to its institutional organization, it allows us to infer party mobility and the formation of new parties together and, if the latter is known, it also allows us to have a clearer view of the institutional reality in a joint analysis.

The second index is the EDP. It measures the electorate’s level of general preference concerning parties. It indicates whether there is a historical preference on the part of voters, or whether there is a change. In other words, it shows the level of acceptance of the parties and their configurations, that is, of the status quo political. Thus, the average age measures the internal organization of parties globally and the EDP measures the level of acceptance of parties globally. One index is associated with internal party issues and the other is linked with the level of acceptance by voters, that is, a measure external to the parties. In this way, the Party Institutionalization Index (Tp) is calculated. It considers a factor internal to the parties (average age) and another factor, this external to them (EDP).

Equation: Equation 23 calculates the IP.

TO BE CONTINUED…

8.6: Number of New Parties Criterion

Concepts: This is not an index, but an idea that, based on some assumptions, allows new parties (NP) to be counted. The idea was proposed by Sikk, in 2005. To count as a new party, the following premises must be met in their entirety, they are:

1: It is considered a new party when it is not a succession of another party, having emerged per se.
2: It is considered a new party when a new name is given.
3: A new party is considered when it has its structure, created for this purpose, and does not have a structure acquired from another party.
4: It is considered a new party when it doesn’t originate from existing party mergers or electoral coalitions.
5: It is considered a new party when filling all four previous criteria, it has obtained at least 0.5% of votes.
6: Independent parties are not considered a new party.

Thus, in this way, new parties are counted based on the mentioned criteria. As can be seen, it prioritizes party innovation, that is, mobilization and innovation within the party system.

9: Analysis of Party Behavior

They are analyses carried out to verify the degree of cohesion of parties within a legislative house or a party.

9.1: Party Discipline Index

Proposition: This index has several proponents because it is presented in different forms. Each of the forms considered had a different thinker.

Equation: In the present case we have three distinct equations, with a similar general idea, however, applied to different situations, resulting in; therefore, other values ​​for the index. The equations are presented generically, according to equation 24.

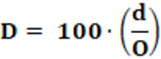
Concepts: The Party Discipline Index (D) can be presented with other terminologies, such as Party Loyalty Rate; and other denominations. The index indicates the idea of ​​unity of a party’s action, in votes in a legislative house, as long as there is prior guidance from the party leadership which, in theory, should be followed by its parliamentarians.

The party discipline index has this name because it measures, in percentage form, the obedience of parliamentarians to their parties in terms of following voting guidelines, that is, voting as directed by the leaders and the official position of their party in the legislative house. Therefore, the index measures discipline within the party, that is, institutional obedience to the party. In other words, the D index is based on an institutional rule that the party expects its parliamentarians to follow. The voting; therefore, isn’t spontaneous and measures, in political practice, not party discipline, based on the parliamentarians, but rather the force that that party exerts over its parliamentarians. In other words, it measures the coercive force of each party over its parliamentarians.

It can also measure party loyalty, as long as parliamentarians assume their position and it is under the party’s institutional orientation. In this case, it measures ideological acceptance and agreement. Conceptually, party loyalty and party discipline are distinct. This is because, in party discipline, the vote guided by the party is followed by the parliamentarian even if he does not agree, whereas, in party loyalty, the parliamentarian votes under the party’s orientation. After all, he agrees, ideologically, with the proposed idea. They vote by agreement and not by coercion. However, as it is difficult to obtain data on voting intentions, the obvious and common thing is to get data from the votes cast; because these are visible, then the party discipline index is calculated and this is adopted as the same party loyalty index, however, as discussed, they are conceptually different indices. In short, party discipline measures party coercion and party loyalty measures spontaneous action by the parliamentarian. The first comes from the party towards the parliamentarian and the second comes from the parliamentarian towards the party.

With this clarification, the analysis follows for each of the equations and its changes, according to equation 25. The first thing to address is that “d” represents the number of times that the parliamentarian followed party discipline, voting, in the legislative house, under the guidance received by the party. This parameter is constant. What changes is the parameter “O” which can have three different values, namely: “(OP)–“, used when the parliamentarian was present in the legislative house and there was guidance from the party to vote “yes” or “no” (equation 25a); “(OT)–“, used whenever the party oriented the vote in the legislative house only as “yes” or “no”, regardless of the presence of the parliamentarian in the house (equation 25b) and “(OT)+“, used whenever the party oriented the vote in the legislative house in any direction, including in addition to “yes” and “no”, also obstructions, regardless of the presence of the parliamentarian in the house (equation 25c).

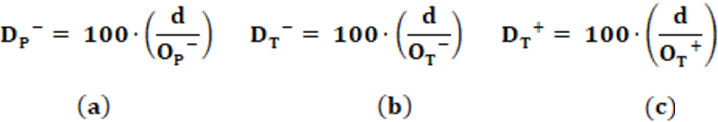
Given the equations, we can easily say that (OP)^– < (OT)^– because (OT)^– considers the presence or absence of the parliamentarian, which means that (OP)^– is less than or at most equal to (OT)^–, which occurs when the parliamentarian was not absent when the party carried out the voting guidance. Similarly (OT)^– < (OT)⁺ because (OT)⁺ considers all guidelines, not just voting “yes” or “no”. So; we have: (DP)^– > (DT)^– > (DT)⁺ . The D index must be calculated within a given period not just in a single vote. An important observation about the D index is that low values ​​indicate party indiscipline, which may indicate an intra-party crisis.

An interesting observation is adopting a cutoff margin for cases where the majority was solid in the legislative house. For example, in cases where 90% of parliamentarians voted the same way, in this case, party discipline is not a measure that can provide a real measure, since there was no conflict, a moment where party discipline is an important measure to be measured.

Interpretation: The interpretation of the D index is straightforward and seen through the calculated percentage value. High values ​​indicate high party discipline and low values ​​indicate low party discipline. Values ​​above 90% are common. Values ​​below this percentage are rare.

Input data: To determine the D index, it is necessary to have access to the votes of parliamentarians and the nomination of the parties, as well as the comparison of this information to estimate the parameter “d”.

Example: Based on the data in table 6, considering that column 1 corresponds to parliamentarians from the same party, which +1 corresponds to a vote in the same direction as the orientation of the party leaders; that -1 corresponds to a vote contrary to that guided by the party leaders and 0 is when the party leaders did not guide the vote, thus, we have: Parliamentary 1; 3/4 = 75%; Parliamentarian 2; 4/4 = 100%; Parliamentarian 3; 3/4 = 75%; Parliamentarian 4; 1/4 = 25%; Parliamentarian 5; 3/4 = 75%; Parliamentarian 6; 1/4 = 25%; Parliamentary 7; 3/4 = 75%; Parliamentary 8; 2/4 = 50%. This is party discipline for each parliamentarian. This is a result. Taking the arithmetic average of the party discipline values ​​of each parliamentarian, we have the party discipline, assuming that there are 8 parliamentarians. Thus, we have party discipline at 62.5%.

9.2: Rice Index of Intraparty Cohesion

Proposition: The name of the Rice (R) index is a tribute to the American statistician and sociologist Stuart Arthur Rice, its creator.

Equation: The equation that calculates the R index is presented in equation 26.

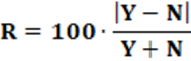
The same equation 26, after algebraic manipulations can be rewritten as presented in equation 27.

Concepts: The Rice (R) index is also known as the Party Cohesion Index; Intraparty Cohesion Rate; Party Unity Rate and any other tax that confers the idea of ​​agreement on votes in the legislative house by parliamentarians from any party. This index does not assume that there is prior guidance from the party leadership to its parliamentarians. Therefore, it differs, conceptually, and mathematically, from the party discipline index (D). It can also be expanded to include cohesion within the legislative house, becoming an inter-party index.

This occurs because the parliamentarian’s vote is spontaneous, without coercion based on party orientation. Even if there is party orientation and the parliamentarian votes according to his own will, the fact that there is an orientation affects the value of the R index because other parliamentarians may change their voting intention depending on the party’s orientation.

Therefore; The R index is only valid when there is no party orientation for voting in the legislative house. The idea is to indicate the value of party cohesion among parliamentarians, which is a spontaneous measure, free from coercion by the party itself. Cohesion allows, by inference, to estimate the level of party loyalty (not to be confused with party discipline). The great value of the R index is that it allows us to check, in situations free from institutional pressure, the unity of thought and decision-making of parliamentarians from the same party. It enables us to infer based on the value of the R index, an intra-party and ideological crisis.

Interpretation: The interpretation of the R index, like the previous case, is direct and seen through the calculated percentage value. High values ​​indicate high party cohesion and low values ​​indicate low party cohesion.

Input data: To determine the R index, it is necessary to have only the percentage number of “yes” votes. With this information, the “R” parameter is estimated.

Example: From the data in table 6, considering that column 1 corresponds to parliamentarians from the same party, which +1 corresponds to a “YES” vote to a given bill, which -1 corresponds to a “NO” vote to the same bill, and disregarding the columns marked “0”; so we have. Bill 1: Y = 6, N = 2; Bill 3: Y = 7; N = 1; Bill 4: Y = 5, N = 3; Bill 5: Y = 5, N = 3. The next step is to estimate the percentage of “Y” for each Bill, so we have; Y1 = 100 x (6/8) = 75%; AND3 = 100 x (7/8) = 87.5%; AND4 = 100 x (5/8) = 62.5%; AND5 = 100 x (5/8) = 62.5%. If the arithmetic average of these four votes is taken, we will have the R index of these four votes, which results in 71.87%. The analysis can be done for a party (intra-party) or the entire legislative house (parliament).

10: Government Analytics (Executive)

These are analyses carried out to analyze the government, regarding its ability to govern and level of parliamentary acceptance, as well as the strength of a government and its popular acceptance.

10.1: Percentage Polarization Index

Proposition: Polarization can be measured simply way and with a certain degree of confidence, although non-linear or unforeseen political aspects can affect the confidence of this measure. The Percentage Polarization Index (POL) was proposed in 1976 by Sartori (Giovanni Sartori; Political Scientist – Italy).

Equation: The equation that calculates the POL index is presented in equation 28.

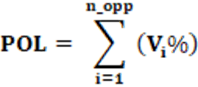
Concepts: Conceptually, polarization is measured according to the percentage that opposes the incumbent government. If the equation uses the total number of seats in the legislative house won by opposition parties, the polarization is legislative. If the equation uses the votes of voters granted to these parties, this represents the polarization that exists in society. This is the case in equation 28. Polarization is indicated by n_opp; where “n” considers all parties in an election, while “n_opp” only considers opposition parties.

For a party to be categorized as an opposition party, it must simultaneously meet three criteria. They are: 1: It is a party that stands in opposition to the parties that make up the parties that support the government. 2: The party has a discourse stating that there is a distance between politics and society. 3: Affirm and work to change the status quo, to bring about major changes in politics and the political system. Therefore, all party that meets the criteria is considered an opposition party. Every opposition party enters the sum of equation 28.

Interpretation: The interpretation of the POL index is simple and straightforward. The resulting value of the POL index is the percentage value of polarization. Remember that equation 28 uses the percentage of votes, which represents the polarization of society towards the government and parties that support it. If the percentage number of seats in the legislative house is used, this polarization is legislative, as already stated.

Input data: To calculate the POL index, only one piece of data is needed, and that is the number of votes obtained by each party, in percentage terms (Vi%). After that, the three opposition criteria must be applied. Once these are filled in, equation 28 applies. This is how the POL index is calculated.

Example: From the data in table 6, considering that column 1 corresponds to parties, that the sign (+) corresponds to a party in favor of the government and (-) corresponds to an opposition party, polarization occurs based on the sum that each opposition party received in the elections, which is detailed in the last column. Thus, polarization considers parties A, C, F, and H; whose polarization value is 55.3%.

10.2: Coalescence Rate

Concepts: The coalescence rate (M) also known as Ministerial Cabinet Rate measures the difference in the proportion between the number of parties’ seats in parliament and the proportion of parties in ministries. In other words, it measures the level of party proportion in parliament and ministries. For the motivations of the executive branch, the ideal is that the index is zero, moment, and that pi = mi. There is no specific equation to calculate the Coalescence Rate. For this purpose, any equation that calculates indices can be used to verify the proportionality or disproportionality of the representation of parties in the electoral system. This includes the linear deviation, quadratic deviation, and overrepresented value indices equations.

To do this, it must be clear that, conceptually, the coalescence rate calculates the absolute difference between the proportion of ministries that a party has and the proportion of seats that the same party has in parliament. Therefore, for the calculation, we must use indices that calculate proportionality. In this sense, the only direct index in use is the Rose index (RO), which calculates the proportionality of party representation in the electoral system. For the other indices, use is not straightforward because they calculate disproportionality, and, to use them, we have to make a small transformation, which is to subtract the result from 1.

Furthermore, other than that, in either case, the value vi is replaced by mi, and pi is held. We must understand that mi is the proportion of ministries of the party I.

Equation: For illustration purposes, equation 29 is presented with its changes, for the Rose index, which in this case is indicated as ROm. The Gallagher index adapted for the case is presented, which must be done for all other disproportionality indices. The Gallagher index indication for this case is LSqm.

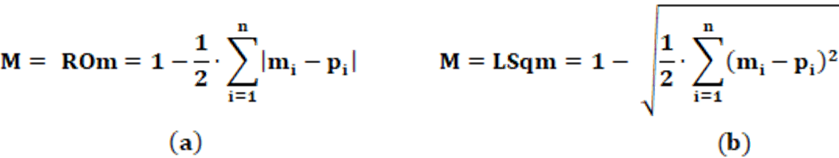
Interpretation: The interpretation of the obtained value is straightforward when using the Rose index and must be mirrored when another index is used. Of course, the M index varies in value depending on the equation used. This is the same calculation of indexes for party representation in the electoral system. The ideas with advantages and disadvantages of indices are equally applied here.

Example: From the data in tables 6 and 7; using the equation M = ROm; and considering the year 2020; we can calculate the coalescence rate. The first is to be clear that the percentage values ​​in table 6 must be transformed into indices, that is, divided by 100. The second step is to calculate the proportion of seats for each party, as follows: Party A, pi = 10/25 = 0.4; Party B, pi = 6/25 = 0.24; Party C, pi = 4/25 = 0.16; Party D, pi = 3/25 = 0.12; Party E, pi = 2/25 = 0.08. The third step is to calculate the absolute difference for each party; Party A, |vi-pi| = 0.08; Party B, |vi-pi| = 0.055; Party C, |vi-pi| = 0.192; Party D, |vi-pi| = 0.109; Party E, |vi-pi| = 0.058. The fourth step is to realize the calculation of the coalescence rate which comes out to be 0.753 (75.3%).

10.3: Presidential Support Assessment

Concepts: The Presidential Support Rating (GOV) is a percentage measure that indicates the level of support that the executive branch has with the legislative branch. The GOV index measures the strength and prestige of the executive and its government. It allows for identifying the president’s ability to govern. Support for the executive is related to votes in parliament, generally the Federal Chamber of Deputies; therefore, it is used as a reference for comparative policy purposes. The idea is simple and we must consider that the index must be measured from a certain period. It is interesting to do a monthly analysis and have this information presented in a graph for easy visual interpretation of the data, over a year. The index is calculated based on the relationship between votes in favor of the government concerning total votes. The value is presented in percentage form.

Equation: The equation has the same idea for measuring party discipline. It is shown in equation 30.

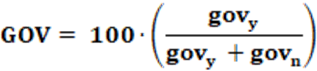
Interpretation: The interpretation of the value is straightforward. High values ​​of the GOV rate indicate greater legislative support for the executive and better governance, with lower political costs and less prone to crises. Low values ​​of the GOV rate indicate less legislative support for the executive and more difficult governance, with greater political costs and a greater probability of crises.

Input data: To estimate the GOV rate needs of the votes in each legislature for and against the government. You must know the government’s orientation for each one of the votes. The values ​​must cover a certain period, otherwise the rate will not reproduce reality. Give preference to votes where there is opposition, otherwise, the GOV rate will not reproduce reality.

Example: From the data in table 6, considering that column 1 corresponds to parliamentarians from different parties, +1 corresponds to a vote in favor of the government’s expectations for a given bill, and -1 corresponds to a vote against the government’s expectations for a given project of Law, and considering that the columns marked “0” represent government indifference; so we have. Bill 1: govand = 6, govn = 2; Bill 3: govand = 7; govn = 1; Bill 4: govand = 5, govn = 3; Bill 5: govand = 5, govn = 3. Thus, we have; Bill 1, GOV = 75%; Bill 3, GOV = 87.5%; Bill 4, GOV = 62.5%; Bill 5, GOV = 62.5%. In this case, as the data in the table are the same, the GOV index values ​​resulted in the same values ​​as the intra-party cohesion rate, however, with real data, this is unlikely to happen. Finally, we can take the arithmetic average to estimate the GOV index, which results in 71.87%.

10.4: Political-Institutional Performance Assessment

The first thing to inform is there is no single index or a single rate that measures the Political-Institutional Performance Assessment, represented, in a generic way, by the Greek letter ε. There are several ways to carry out this measurement. There are measures taken by all countries because they have a technical, logical, and practical nature, such as inflation, unemployment rate, annual growth rate, and domestic product, among others. These are analyses of the economy and related areas.

There are also measures created to compare results between countries, such as the Gini and the PISA index. Other indices make comparative measurements between countries. There is, for example, the happiness index.

In our case, it is only important to point out that an ε analysis must consider several areas of government activity because the evaluation is of the performance of the executive branch. Of course, there is no single index. For a more effective analysis, it is interesting to separate the analyses into three categories: management indicators; strategic indicators, and operational indicators. This way we have a better elaborated vision and analysis that is more in tune with reality. These indicators are categorized as hierarchical indicators.

Any indicator must meet three basic requirements: i – realize methodical data collection; ii – it must also have data collected periodically and iii – it must represent the reality of what it measures. Furthermore, the analysis must be cumulative and needs to generate data on the timeline, for better interpretation. Regardless of the index and what it measures, the indexes must meet these requirements.

One of the professionals who must work on preparing indices for government analysis are the Political Scientists. However, indicators constructed by economists, mathematicians, statisticians, and engineers are common.

10.5: Party System Closure Index

Concepts: The Party Closure index (X) indicates how open a party system is to change. It is measured through ministerial changes and the parties that assume these positions. The X index is a temporal index and considers the history of changes. Three elements are used in the calculation of the X index, they are: alternation; formula, and access.

Alternation (ALT) refers to the difference in ministerial cabinets obtained by each party between consecutive ministerial compositions (consecutive elections). In other words, we must consider the election e and the election e-1 and its ministerial compositions. The calculation is similar to Pedersen’s index, however, the difference is that we use the ministerial portfolios of each party. As stated, the difference considers two consecutive elections (ministerial compositions) using all parties in the calculation, those that remain with cabinets in election e and those who only had cabinets in election e-1. The calculated value is the alternation value. This value must always be between 50 and 100, if it is less than 50, we must subtract this value from 100, and this will be the result of the alternation, otherwise, the calculated value is the alternation value itself.

In second place the Formula (FOR) is related to innovation in government it is the constitution that the government uses to compose ministries. The formula has three types of values. If there is total innovation, which occurs when there is no repetition of parties making up the same party group in ministries, the value of the formula is 0. This happens when the composition is unique within the period analyzed. When isn’t there innovation that occurs when in the analyzed election the parties are recurrent at some point in the past, the value will be 100, as long as in the analyzed election these parties are repeated in their entirety or only part of it. If the repetition of parties is total or partial, but there is the arising of a new party that creates a new composition in the ministries; something that has not yet occurred, the value of the formula is the sum of the percentage values ​​of the recurring parties. In the latter case, the formula is not innovative or without innovation, but partial innovation. Therefore, the value will always be greater than 0 and less than 100.

Finally, Access (ACC) has a similar idea to the Formula, however, instead of considering party groups, it considers party access to ministries. Access will have a value of 0 if the access is from parties that have never held ministerial positions. Access will have 100 if all parties already have access to ministerial cabinets. If part of the parties have had access and another part doesn’t have access, the value of access will be the sum of the percentages of the parties that have already had access to the ministries, that is, it disregards the parties that have access for the first time. Similar to the formula, access uses recognizing recurrences and not new developments.

At the end of these values, we calculate the average of each of these three values. From the alternation average, we apply a correction, since the scale is between 50 and 100 and we must correct to a scale of 0 to 100. To do this we apply equation 31. Once this is done, we apply equation 32 and obtain the value of the closure index of the party system (X).

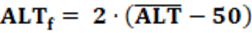
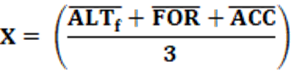
The Party System Closure index (X) allows for measuring the Institutionalization of the Party System (PSI). This index is of great value for deeper analyses of parties and party systems. There are several possibilities for measuring PSI, and one of them is the X index, which brings good results because the calculations include party fragmentation, electoral volatility, stability of the party, and electoral system, among others. That is why the X index is one of the most used models to measure the institutionalization of the party system (PSI). The PSI value is the calculated X value.

Interpretation: Reading the value is straightforward. The closer to 100%, the greater the closure of the party system, that is, the system does not allow innovations both in the composition of parties and in their group compositions. It also considers little variation in the proportion of ministries. For low values, this indicates a great openness to change. Values ​​above 80% are common.

Input data: To calculate the X index we need the number of ministerial offices each party has during the period to be analyzed. This value must be in percentage form.

Example: For analysis purposes, we present the data in table 8 to facilitate the study. Next to it are the alternation results; formula and access. Below we have the relevant explanations.

i	Year(Election)	Ministries and Parties (%)	ALT	FOR	ACC
1	1986 (1)	A = 50; B = 20; C = 10; D = 10	FG	FG	FG
2	1987	—	100	100	100
3	1988	—	100	100	100
4	1989	—	100	100	100
5	1990 (2)	A = 55; B = 25; C = 20	85	100	100
6	1991	—	100	100	100
7	1992	—	100	100	100
8	1993	—	100	100	100
9	1994 (3)	E = 100	100	0	0
10	1995	—	100	100	100
11	1996	—	100	100	100
12	1997	—	100	100	100
13	1998 (4)	B = 25; E = 55; F = 20	55	0	80
14	1999	—	100	100	100
15	2000	—	100	100	100
16	2001	—	100	100	100
17	2002 (5)	A = 45; B = 15; G = 40	85	60	60
18	2003	—	100	100	100
19	2004	—	100	100	100
20	2005	—	100	100	100
21	2006 (6)	A = 30; H = 30; I = 40	70	0	30
22	2007	—	100	100	100
23	2008	—	100	100	100
24	2009	—	100	100	100
25	2010 (7)	A = 30; H = 50; J = 20	60	80	80
26	2011	—	100	100	100
27	2012	—	100	100	100
28	2013	—	100	100	100
29	2014 (8)	A = 20; B = 45; K = 35	80	65	65
30	2015	—	100	100	100
31	2016	—	100	100	100
32	2017	—	100	100	100
33	2018 (9)	A = 25; E = 15; F = 60	80	0	100
34	2019	—	100	100	100
35	2020	—	100	100	100
36	2021	—	100	100	100
37	2022 (10)	C = 15; D = 25; E = 20; F = 40	55	100	100
38	2023	—	100	100	100
39	2024	—	100	100	100
	TOTAL	—	3.570	3.305	3.515

Explanation of example values: The first is to indicate a reference year that we call the Financing Government, marked as FG. This corresponds to the beginning of the analysis. The second point is to check the periods between elections. In these periods there are no changes, so we mark it as 100 for all three elements in the periods between elections. For the others, we have to carry out the relevant analyses.

ALTERNANCE: Corresponds to the application of the Pedersen equation adjusted to the present situation, thus we have: (1990): ALT = (1/2) x |(55-50)+(25-20)+(20-10)+(0 -10)| = 15. Like 15<50; so, 100-15 = 85. (1994): ALT = (1/2) x |(100-0)+(0-55)+(0-25)+(0-20)| = 100. (1998): ALT = (1/2) x |(55-100)+(25-0)+(20-0)| = 45. Like 45<50; so, 100-45 = 55. (2002): ALT = (1/2) x |(45-0)+(15-25)+(0-55)+(0-20)+(40-0) | = 85. (2006): ALT = (1/2) x |(30-45)+(0-15)+(0-40)+(30-0)+(40-0)| = 70. (2010): ALT = (1/2) x |(30-30)+(50-30)+(0-40)+(20-0)+(40-0)| = 40. Like 40<50; so, 100-40 = 60. (2014): ALT = (1/2) x |(20-30)+(45-0)+(0-50)+(0-20)+(35-0) | = 80. (2018): ALT = (1/2) x |(25-20)+(0-45)+(15-0)+(60-0)+(0-35)| = 80. (2022): ALT = (1/2) x |(0-25)+(15-0)+(25-0)+(20-15)+(40-60)| = 45. Like 45<50; so, 100-45 = 55.

FORMULA: Corresponds to party groups. (1990): How parties A, B, and C appear in 1986; so there was no innovation in the composition, therefore, 100. (1994): As party E never appeared, being a unique configuration, then there was innovation in the composition, therefore, 0. (1998): As the configurations B, E, and F are unique, so there was innovation in the composition, therefore, 0. (2002): Configuration A, B, G did not exist until then, however, configuration A, B; Yes; there is partial innovation; therefore, the formula is the sum of the percentages of A and B, therefore 60. (2006): As configuration B, E, F is unique, there was innovation in the composition, therefore, 0. (2010): Configuration A, H, J until then did not exist, however, the A, H configuration; Yes; there is partial innovation; therefore, the formula is the sum of the percentages of A and H, therefore 80. (2014): The configuration A, B, K did not exist until then, however, the configuration A, B; Yes; there is partial innovation; therefore, the formula is the sum of the percentages of A and B, therefore 65. (2018): As the configuration A, E, F is unique, there was an innovation in the composition, therefore, 0. (2022): Here we have two configurations recurring, C, D and E, F. Thus, from the sum of the percentages we have 100.

ACCESS: Corresponds to parties and access to ministries. (1990): The same parties in 1990 were the same as in 1986, so the same parties had access to ministries; therefore, 100. (1994): Party E had its first access to the ministries. (1998): The only new party is F, so access is given by the sum of the percentages of the other parties, therefore, 80. (2002): The only new party is G, so access is given by the sum of the percentages of the other parties, therefore, 60. (2006): There are two new parties, H, and I, so access is given by the percentage of A, therefore, 30. (2010): The only new party is J, so access is given by the sum of the percentages of the other parties, therefore, 80. (2014): The only new party is K, so access is given by the sum of the percentages of the other parties, therefore, 65. (2018): There is no party new to ministries; therefore, 100. (2022): There is no new party in the ministries; So, 100.

With these values, we calculate the average of the three values, which results in ALT = 91.53; FOR = 84.74; ACC = 90.12. The value of ALTf from equation 31, is 83.06. Finally, we apply equation 32 to obtain X, which results in 85.97%.

10.6: Index of a Country’s Military Power

Proposition: The Country Military Power Index (MW) was created in 2011, and proposed by Sulek (Mirosław Sułek; Economist – Poland). The index measures the military strength of a country based on relative values ​​and, as a result of its conceptualization, through comparative values ​​between countries, which suggests a clear idea of ​​military power, measuring military strength.

Equation: Equation 33 presents the calculation (adapted presentation).

Concepts: The index evaluates the military strength of a given country based on relative values ​​between the values ​​of all countries on the globe, in base 1000. Thus, the index is a relative index which suggests a direct comparison, an advantage of the index. The GDPM parameter is the military expenditure of the analyzed country, in terms of GDP. It is a relative value, as it considers, for the same year, the relationship between military spending, in terms of the national GDP of the country analyzed, concerning global expense, in terms of world GDP, of all countries, which is conceptually worth 1000.

We must apply the same idea to the other two parameters. The MIL parameter is the relationship between the number of active military personnel in the analyzed country and the number of active military personnel in the world whose assigned value is 1000. In the same reasoning, S is the relative area country concerning the habitable area of the planet (sum of the area of ​​the five habitable continents), whose assigned value is 1000.

In this way, based on the country ​​and global values through simple proportion, we obtain the relative values ​​in base 1000. These are the values ​​that should be used in equation 33. The idea is to have an index that measures military power and expenses, and the number of active military personnel allowing a direct relationship when reading the index. The territorial area is the area of ​​military activity of the analyzed country. This area is where the government exercises its military power. The larger the area of ​​the country, the larger the area of ​​military action.

Interpretation: The interpretation is direct reading. The higher the index, the greater the military power. We must remember that the index is constructed from relative values. Therefore, the index infers a relative measure of military power.

Input data: For the calculation, it is necessary to have the value of military spending in the country to be analyzed in terms of GDP, as well as the total amount spent in the world. We must have the area of ​​the analyzed country and the area of ​​the five habitable continents, data that is simple to obtain and has fixed values, except for geographical changes. Finally, we have to have the number of active military personnel, in the country analyzed and the world. These values, with changing from year to year, don’t have significant changes.

Example: For this example, we do not have a table, we will use the values ​​indicated directly here. In this case, for any year, consider a country with a territorial area of ​​5,000,000 km2; military expenditure worth US$450,000,000, and with a contingent of 300,000 active military personnel. In global terms, military spending this same year was US$1,500,000,000,000; the number of active military personnel is approximately 20,500,000 and the area of ​​the 5 continents is around 135,000,000 km2; the value of the W index is as follows. The first to estimate is GDPM whose calculation is (U$ 450,000,000/ U$ 1,500,000,000,000) x 1000 = 0.3. The second estimate is the MIL whose calculation is (300,000 military personnel / 20,500,000 military personnel) x 1000 = 14.63. Finally, S is estimated, calculated like this, (5,000,000 km2/ 135.000.000 Km2) x 1000 = 37.03. With these values, ​​we calculate W, which results in 1.21.

11: Some Relationships between Indices

Indexes can be calculated from others as they are related to each other. Possible relationships follow.

Relations between RAE and ENP.

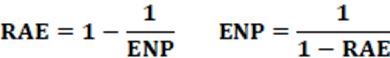
Relations between RAE^D; LH; RO and G.

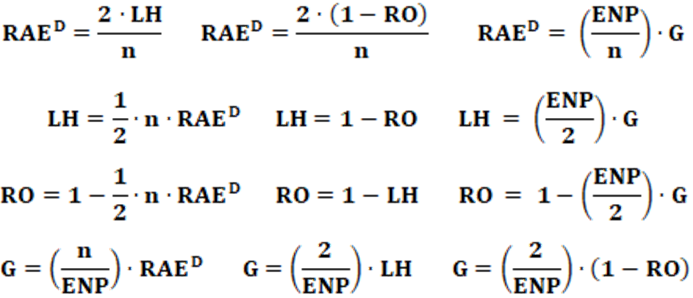
Relations between LSq and MO.

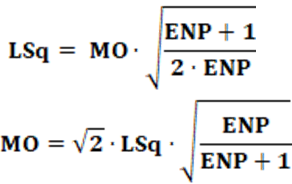
12: Practical Results

Now, we present values and results real ​​for Brazil.

RAE: 0,89 (year, 2022) – 89%	MD: (year, 2022)	PI: **
ENP: 9,2 (year, 2022)	LJ: (year, 2022) *	NP: Partido Novo, in 2015 (year, 2024)
RAED: 0,1009 (year, 1998) – 10,09%	DH: (year, 2022) *	D: 83% (PDT, more undisciplined; year 2019)
LH: 0,0913 (year, 1998) – 9,13%	W: 74,78% (year, 2022 – presidential elections, 1st round)	R: 84,1% (years, 2011-2014)
RO: 0,9087 (year, 1998) – 90,87%	GAP: 1,8% (year, 2022 – presidential elections, 2nd round)	POL: 49,10% (year, 2022 – presidential elections)
G: 0,02571 (year, 1998) – 2,57%	P: (year, 2022) **	M: 39% (year, 2018)
LSq: 3,53 (year, 2022)	LW: (period, 1998/2022; year 2022) **	GOV: 47% (year, 2024 until June)
SL: *	EDP: (period, 1998/2022; year 2022) **	X: **
MO: 4,74 (year, 2022)	Tp: 24 years and 5 months (year, 2024, month 07)	MW: 7,2

13: Conclusions

The indices and analyses presented allow through values to identify aspects of institutional policy and comparative analysis between countries. The idea doesn’t end with the presentation of these indices. Many others exist and others are created by researchers who seek to facilitate the interpretation of political reality through quantitative analysis, which provides an intuitive interpretation.

We should not compare indices with each other and with their final values. This has two reasons, the first is that each one has its particular construction, with sensitivities to different variations on the stimulus and the response that variations provide in the result. Secondly, they are on different scales thus the direct comparison is a conceptual error. Therefore, the comparison of indices is for individual analysis and comparison between countries, but not between indices, except to carry out technical analyses.

The use of indices should be used for deeper analysis and should be disseminated and encouraged for use in academic and professional circles. Encouraging use in academia is the right path for use in professional circles. Thus, politics finds a source of response to its variations and responses in the social environment in a more intuitive way.

BIBLIOGRAPHIC REFERENCES

AIKATERINI, Kalogirou. Analysis and Comparison of the Greek Parliamentary Electoral Systems of the Period 1974-1999, chapter 5.
ARREDONDO, Verónica; MARTÍNEZ-PANERO, Miguel; PALOMARES, Antonio; PEÑA, Teresa; RAMÍREZ, Victoriano. NEW INDEXES FOR MEASURING ELECTORAL DISPROPORTIONALITY. Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA. Volumen 21(2020). Páginas 161 a 178; 2020.
BÉRTORA, Fernando Casal. POLITICAL PARTIES OR PARTY SYSTEMS? ASSESSING THE “MYTH” OF INSTITUTIONALIZATION AND DEMOCRACY.
BÉRTOA, Fernando Casal; ENYEDI, Zsolt; MÖLDER, Martin. PARTY AND PARTY SYSTEM INSTITUTIONALIZATION: WHICH COME FIRST? Cambridge University Press on behalf of the American Political Science Association; 2023.
COLLIRI, Tiago. EVALUATING PRESIDENTIAL SUPPORT IN THE BRAZILIAN HOUSE OF REPRESENTATIVES THROUGH A NETWORK-BASED APPROACH. University of Sao Paulo, Brazil
DEWAN, Torun; SPIRLING, Arthur. STRATEGIC OPPOSITION AND GOVERNMENT COHESION IN WESTMINSTER DEMOCRACIES. 2010.
DUTTA, Bhaskar. THE FRAGMENTED LOK SABHA: A CASE FOR ELECTORAL ENGINEERING. University of Warwick; 2009.
ENAP. ELABORAÇÃO DE INDICADORES DE DESEMPENHO INSTITUCIONAL. Brasília, 2013.
FARID, Wadjdi, A.; MISTIANI; NEBULA F., Hasani. THE MULTI-PARTY SYSTEM IN INDONESIA: REVIEWING THE NUMBER OF ELECTORAL PARTIES FROM THE ASPECTS OF THE NATIONAL DEFENSE AND SECURITY. Journal of Social and Political Sciences, Vol.3, No.3, 711-724; 2020.
FRANZ, Paulo; FERNÁNDEZ, Virginia; CODATO, Adriano. FEDERALISMO E COALIZÃO REGIONAL: A REPRESENTATIVIDADE DOS ESTADOS DA FEDERAÇÃO NOS GABINETES MINISTERIAIS BRASILEIROS. 42º Encontro Anual da ANPOCS, Caxambu-MG; 20218.
FREITAS, Carlos Eduardo de Morais. GRAUS DE COESÃO PARTIDÁRIA NO BRASIL: OS NÍVEIS DE CONVERGÊNCIA PROGRAMÁTICA DAS ELITES PARLAMENTARES SUBNACIONAIS. UFMG, Belo Horizonte-MG; 2015.
GALLAGHER, Michael. PROPORTIONALITY, DISPROPORTIONALITY AND ELECTORAL SYSTEMS. Trinity College; Dublin, Ireland; 1991.
HANDLEY, Lisa. SOME MATHEMATICAL MEASURES FOR DETERMINING IF A REDISTRICTING PLAN DISPROPORTIONALLY ADVANTAGES A POLITICAL PARTY. Michigan University, USA.
HIX, Simon; NOURY, Abdul; ROLAND, Gérard. POWER TO THE PARTIES: COHESION AND COMPETITION IN THE EUROPEAN PARLIAMENT, 1979-2001. Cambridge University Press, UK.
KESTELMAN, P. APPOTIONMENT AND PROPORTIONALITY: A MEASURED VIEW.
LAAKSO, Markku; TAAGEPERA, Rein. EFFECTIVE NUMBER OF PARTIES: A MEASURE WITH APPLICATION TO WEST EUROPE. University of California, Irvine; 1979.
MACKIE, Thomas T. UNITED KINGDOM. European Journal of Political Research, Netherlands; 1995.
MAINWARING, Scott. PRESIDENTIALISM, MULTIPARTY SYSTEMS, AND DEMOCRACY: THE DIFFICULT EQUATION. 1990.
MARTÍNEZ-PANERO, Miguel; ARREDONDO, Verónica; PEÑA, Teresa; RAMÍREZ, Victoriano. A NEW QUOTA APPROACH TO ELECTORAL DISPROPORTIONALITY. MDPI, 2019.
PAIVA, Denise; PIETRAFESA, Pedro A. SISTEMAS PARTIDÁRIOS, PARTIDOS E ELEIÇÕES. TENDÊNCIAS E DINÂMICAS NA FEDERAÇÃO BRASILEIRA 1998-2018. Puc Goiás, Brasil; 2022.
PETRY, Eric. HOW THE EFFICIENCY GAP WORKS. Brennan Center for Justice.
PIÑEIRO, Rafael. Election of Representatives and party fractionalization in Uruguay 1942-1999. Revista Uruguaya de Ciencia Política, 2004.
RIBEIRO, Pedro Floriano; LOCATELLI, Luís; ASSIS, Paulo Pedro de. ACOMPANHO O MEU PARTIDO: ORGANIZAÇÃO PARTIDÁRIA E COMPORTAMENTO LEGISLATIVO NO BRASIL. Artigos Originais; Rio de Janeiro; 2022.
ROSE, Richard. COMPARING FORMS OF COMPARATIVE ANALYSIS. Political Studies; 1991.
SATOH, Keiichi; GRONOW, Antti; YLÄ-ANTILLA, Tuomas. THE ADVOCACY COALITION INDEX: A NEW APPROACH FOR IDENTIFYING ADVOCACY COALITIONS. Policy Studies Journal; 2021.
SCHEFFLER, Iuna Lamb. DISCIPLINA PARTIDÁRIA: MENSURACÃO, TEORIA E ANÁLISE DE SEUS DETERMINANTES. UFRGS, Porto Alegre; 2019.
STEPHEN, Josh Goldenberg; FISHER, Stephen D. THE SAINTE LAGUË INDEX OF DISPROPORTIONALITY AND DALTON’S PRINCIPLE OF TRANSFERS. University of Oxford University; 2017.
SULEK, Mirosław. WIELOWYMIAROWY SPOSÓB SZACOWANIA PODSTAWOWYCH KATEGORII WOJSKOWYCH PAŃSTW. https://geopolityka.net/, 2011.
TAAGEPERA, Rein; GROFMAN, Bernard. MAPPING THE INDICES OF SEATS–VOTES DISPROPORTIONALITY AND INTER-ELECTION VOLATILITY. PARTY POLITICS VOL 9. No.6 pp. 659–677; 2013.

https://whogoverns.eu/wp-content/uploads/2021/03/Party-institutionalization-150-153.pdf. Accessed June 24, 2024.
https://whogoverns.eu/wp-content/uploads/2021/03/Closure-34-43.pdf. Accessed June 24, 2024.
https://whogoverns.eu/wp-content/uploads/2014/10/EPSA-2014.pdf. Accessed June 24, 2024.
https://whogoverns.eu/party-systems/party-system-closure/. Accessed June 24, 2024.
https://whogoverns.eu/party-systems/party-institutionalization/. Accessed June 24, 2024.
https://www.youtube.com/watch?v=yLqaVKZ4sdw&t=9s. Accessed July 3, 2024.
https://static.poder360.com.br/2023/07/Electoral_Indices_Gallagher.pdf. Accessed June 24, 2024.
https://aceproject.org/main/english/es/esg04.htm. Accessed June 24, 2024.
https://www.scielo.br/j/dados/a/DBLZXnGrZYNZRPYSKDsSGkg/. Accessed June 24, 2024.
https://www.sciencedirect.com/science/article/pii/S0895717708001933. Accessed June 24, 2024.
https://worldpopulationreview.com/country-rankings/gallagher-index-by-country. Accessed June 24, 2024.
https://onlinelibrary.wiley.com/doi/10.1111/j.1467-9248.1991.tb01622.x. Accessed June 24, 2024.
https://cran.r-project.org/web/packages/politicsR/politicsR.pdf. Accessed June 24, 2024.