1: Introdução
Este artigo não tem por objetivo apresentar algo autoral, inovador ou único e sim apresentar, em um único trabalho, os índices clássicos utilizados para análise de política institucional e alguns outros de apresentação recente que possuam relevância conceitual e impacto nas análises. São um total de 28 diferentes abordagens, alguns indicadores com variações.
A ideia é condensar os conceitos e equações com breves explicações e que estas sejam suficientes para entender as diferenças e as aplicações práticas entre os mais variados indicadores. Não são feitas análises em profundidade para os índices, nos limitamos a apresentar os aspectos gerais. A vantagem deste artigo é concentrar os principais índices com as informações mais relevantes, tendo uma visão geral e ampla das mais variadas abordagens existentes.
2: Aspectos Preliminares
Alguns elementos preliminares são necessários para facilitar a leitura deste artigo. Apresentamos, na sequência estes pontos que antecedem o estudo dos índices e demais indicadores.
2.1 – Lista de siglas
Para fins de organização apresentamos as siglas utilizadas neste artigo.
A: Número de abstenção de votos em uma casa legislativa
d: Número de vezes que o parlamentar seguiu a orientação do partido na votação da casa legislativa
govn: Todos os votos que não foram em concordância com o governo na casa legislativa
govy: Número de votos em concordância com o governo na casa legislativa
i: Contador do número de partidos, e outros
m: Proporção de ministérios que o partido conquistou
MIL: Número relativo de militares na ativa, em base 1000
n: Número total de partidos
N: Número de votos “não” em uma casa legislativa, em valores percentuais
nd: Número de vezes que o parlamentar não seguiu a orientação do partido na votação da casa legislativa
O: Número de vezes que o partido orientou os parlamentares para votação na casa legislativa
p: Proporção de cadeiras na casa legislativa ocupadas pelo partido
P: Número de cadeiras na casa legislativa ocupadas pelo partido
PIBM: Gastos militares relativos em base 1000 e em termos de PIB, em determinado ano
S: Área relativa do território, em base 1000, em Km2.
T: Número total de cadeiras na casa legislativa
v: Proporção de votos recebidos pelo partido
V: Número de votos recebidos pelo partido
V+: Número de votos excedentes recebidos em uma eleição
V–: Número de votos perdidos em uma eleição (sem conversão em cadeiras)
Y: Número de votos “sim” em uma casa legislativa, em valores percentuais
Z: Número total de votos na eleição
2.2: Dados de Entrada
Estamos disponibilizando os dados que serão utilizados nos exemplos de cada indicador.
| i | Votos Vi | vi | Vi% | Pi | Pi% |
| 1 | 27.200.000 | 0,2720 | 27,20 | 60 | 24,74 |
| 2 | 24.500.000 | 0,2450 | 24,50 | 55 | 23,73 |
| 3 | 20.040.000 | 0,2040 | 20,40 | 42 | 22,22 |
| 4 | 7.600.000 | 0,0760 | 7,60 | 12 | 9,09 |
| 5 | 6.300.000 | 0,0630 | 6,30 | 9 | 7,07 |
| 6 | 5.900.000 | 0,0590 | 5,90 | 8 | 6,06 |
| 7 | 2.900.000 | 0,0290 | 2,90 | 6 | 4,04 |
| 8 | 2.400.000 | 0,0240 | 2,40 | 3 | 1,51 |
| 9 | 1.900.000 | 0,0190 | 1,90 | 2 | 1,01 |
| 10 | 900.000 | 0,009 | 0,9 | 1 | 0,5 |
| n = 10 | Z = 100.000.000 | Σvi = 1 | ΣVi% = 100 | T = 98 | ΣPi% = 100 |
| i | Pi | pi | pi2 | vi | vi2 | (vi-pi) | (vi-pi)2 |
| 1 | 60 | 0,247474 (= 49/198) | 0,061243 | 0,2720 | 0,073984 | 0,024526 | 0,0006031 |
| 2 | 55 | 0,237373 (= 47/198) | 0,056345 | 0,2450 | 0,060025 | 0,007627 | 0,0000581 |
| 3 | 42 | 0,222222 (= 44/198) | 0,0493826 | 0,2040 | 0,041616 | -0,18222 | 0,0332041 |
| 4 | 12 | 0,090909 (= 18/198) | 0,0082464 | 0,0760 | 0,005776 | -0,02309 | 0,0005331 |
| 5 | 9 | 0,070707 (= 14/198) | 0,0049994 | 0,0630 | 0,003969 | -0,01407 | 0,0001979 |
| 6 | 8 | 0,060606 (= 12/198) | 0,0036730 | 0,0590 | 0,003481 | 0,05294 | 0,0028026 |
| 7 | 6 | 0,040404 (= 8/198) | 0,0016324 | 0,0290 | 0,000841 | -0,01140 | 0,0001299 |
| 8 | 3 | 0,015151 (= 3/198) | 0,0002295 | 0,0240 | 0,000576 | 0,008849 | 0,0000783 |
| 9 | 2 | 0,010101 (= 2/198) | 0,0001020 | 0,0190 | 0,000361 | 0,008899 | 0,0000791 |
| 10 | 1 | 0,005051 (= 1/198) | 0,000025 | 0,009 | 0,000081 | 0,003949 | 0,0000155 |
| n = 10 | T = 198 | Σpi = 1 | Σ(pi)2 = 0,18587 | Σvi = 1 | Σ(vi)2 = 0,19071 | Σ|vi-pi| =0,33757 | Σ|vi-pi|2 =0,03770 |
| i | Vi% | Pi% | Vi% – Pi% | (Vi% – Pi%)2 | (Vi% – Pi%)2/Vi% |
| 1 | 27,20 | 24,74 | 2,46 | 6,0516 | 0,2224853 |
| 2 | 24,50 | 23,73 | 0,77 | 0,5929 | 0,0242000 |
| 3 | 20,40 | 22,22 | -1,82 | 3,3124 | 0,1623725 |
| 4 | 7,60 | 9,09 | -1,49 | 2,2201 | 0,2921184 |
| 5 | 6,30 | 7,07 | -0,77 | 0.5929 | 0,0941111 |
| 6 | 5,90 | 6,06 | -0,16 | 0,0256 | 0,0043389 |
| 7 | 2,90 | 4,04 | -1,14 | 1,2996 | 0,4481379 |
| 8 | 2,40 | 1,51 | 0,89 | 0,7921 | 0,3300416 |
| 9 | 1,90 | 1,01 | 0,89 | 0,7921 | 0,4168947 |
| 10 | 0,9 | 0,5 | 0,4 | 0,16 | 0,1777777 |
| n = 10 | ΣVi% = 100 | ΣPi% = 100 | — | — | Σ= 2,17247 |
| Candidato | Votos – Eleição 1 | Votos – Eleição 2 |
| A | 60.000.000 | 60.000.000 |
| B | 31.000.000 | 31.000.000 |
| C | 7.000.000 | 7.000.000 |
| D | 1.100.000 | — |
| E | 900.000 | — |
| Total | 100.000.000 | 98.000.000 |
| Eleição | Ano | Partido A (1980) | Partido B (1982) | Partido C (1994) | Partido D (2004) | Partido E (2005) | Total |
| 1 | 1994 | 51,2% | 44,3% | 4,5% | — | — | 100% |
| 2 | 1998 | 46,8% | 42,4% | 10,8% | — | — | 100% |
| 3 | 2000 | 30,4% | 42,1% | 27,5% | — | — | 100% |
| 4 | 2003 | 27,2% | 38,5% | 34,3% | — | — | 100% |
| 5 | 2004 | 36,2% | 31,7% | 29,2% | 2,9% | — | 100% |
| 6 | 2008 | 29,4% | 32,9% | 33,0% | 1,8% | 2,9% | 100% |
| 7 | 2010 | 15,9% | 36,7% | 42,5% | 1,7% | 3,2% | 100% |
| 8 | 2012 | 30,1% | 7,8% | 58,3% | 2,3% | 1,5% | 100% |
| 9 | 2016 | 35,6% | 21,5% | 37,8% | 2,3% | 2,8% | 100% |
| 10 | 2020 | 32,0% | 29,5% | 35,2% | 1,1% | 2,2% | 100% |
| Parlamentar/Partido | Voto 1 | Voto 2 | Voto 3 | Voto 4 | Voto 5 | Voto 6 | Votos % |
| A (-) | +1 | 0 | +1 | -1 | +1 | 0 | 27,3 |
| B (+) | +1 | 0 | +1 | +1 | +1 | 0 | 24,3 |
| C (-) | +1 | 0 | -1 | +1 | +1 | 0 | 19,8 |
| D (+) | -1 | 0 | +1 | +1 | -1 | 0 | 9,8 |
| E (+) | +1 | 0 | +1 | +1 | -1 | 0 | 6,2 |
| F (-) | -1 | 0 | +1 | -1 | -1 | 0 | 4,6 |
| G (+) | +1 | 0 | +1 | +1 | -1 | 0 | 4,4 |
| H (-) | +1 | 0 | +1 | -1 | -1 | 0 | 3,6 |
| Ano | Ministérios |
| 1994 | PA: 14; PB: 8; PC: 3; Total de ministérios: 25 |
| 1998 | PA: 14; PB: 8; PC: 3; Total de ministérios: 25 |
| 2000 | PA: 16; PC: 9; Total de ministérios: 25 |
| 2004 | PA: 8; PB: 5; PC: 9; PD: 3; Total de ministérios: 25 |
| 2008 | PA: 8; PB: 6; PC: 4; PD: 3; PE: 4; Total de ministérios: 25 |
| 2012 | PA: 9; PB: 6; PC: 4; PD: 2; PE: 4; Total de ministérios: 25 |
| 2016 | PA: 4; PB: 5; PC: 4; PD: 6; PE: 6; Total de ministérios: 25 |
| 2020 | PA: 10; PB: 6; PC: 4; PD: 3; PE: 2; Total de ministérios: 25 |
2.3: Classificação dos Índices
Para facilitar a compreensão categorizamos as análises e indicadores a partir dos dados utilizados e da forma geral como são calculados. A classificação possui, inicialmente, fins didáticos e pode ser estendida para uma análise mais técnica, porque aspectos técnicos foram considerados para a classificação apresentada.
Para fins didáticos, em nossa categrização temos: 1 – Análises do Sistema Eleitoral; 2: Análises de Mobilidade do Sistema Partidário; 3 – Análise do Comportamento Partidário e 4 – Análise do Governo (Executivo). Estes são divididos da seguinte forma:
1: Análises do Sistema Eleitoral
A – Índices de Ponderação
RAE – Índice de Fragmentação Partidária
ENP – Número Efetivo de Partidos
B – Índices de Desvio Linear
RAED – Índice Rae de Desproporcionalidade do Sistema Eleitoral
LH – Índice Loosemore-Hanby de Desproporcionalidade do Sistema Eleitoral
RO – Índice Rose de Proporcionalidade do Sistema Eleitoral
G – Índice Grofman de Desproporcionalidade do Sistema Eleitoral
C – Índices de Desvio Quadrático
LSq – Índice Gallagher de Desproporcionalidade do Sistema Eleitoral
SL – Índice de Sainte-Lagüe de Desproporcionalidade do Sistema Eleitoral
MO – Índice Monroe de Desproporcionalidade do Sistema Eleitoral
D – Índices de Valores Sobrerrepresentados
MD – Índice de Desvio Máximo de Desproporcionalidade do Sistema Eleitoral
LJ – Índice Lijphart de Desproporcionalidade do Sistema Eleitoral
DH- Índice D’Hont de Desproporcionalidade do Sistema Eleitoral
E – Medidas de Valores de Sobra
W – Voto Desperdiçado
GAP – Lacuna de Eficiência
2: Análises de Mobilidade do Sistema Partidário
EV – Índice Pedersen de Volatilidade Eleitoral
LW – Índice Lewis de Estabilização Partidária
EDP – Índice de Dominância dos Partidos Estabelecidos
Tp – Idade Partidária
PI – Índice de Institucionalização Partidária
NP – Critério de Número de Novos Partidos
3: Análises do Comportamento Partidário
D – Índice de Disciplina Partidária
R – Índice Rice de Coesão Intrapartidária
4: Análises do Governo (Executivo)
POL – Índice Percentual de Polarização
M – Taxa de Coalescência
GOV – Avaliação de Apoio Presidencial
ε – Avaliação de Desempenho Político-Institucional
X – Índice de Fechamento do Sistema Partidário
MW – Índice da Potência Militar de um País
A apresentação dos indicadores é feita através destas categorias e de forma cronológica de surgimento, sempre que a cronologia tenha relevância no desenvolvimento de novos critérios, índices ou indicadores.
3: Índices de Ponderação
São índices que utilizam a proporção de votos de cada partido ou a proporção de assentos conquistados por eles na casa legislativa.
3.1: Índice RAE de Fragmentação Partidária
Proposição: O índice RAE foi criado em 1967, proposto por Rae (Douglas Whiting Rae; Cientista Político – Estados Unidos). O índice mede a fragmentação partidária em um país. O valor numérico pode ser dado na forma de índice, com valores entre 0 e 1 ou pode ser apresentado na forma percentual. O primeiro é mais comum.
Equação: A equação que calcula o índice RAE é apresentado na equação 2. Para o cálculo de pi utilizamos a equação 1.
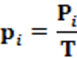
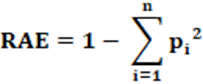
Conceitos: Conceitualmente, o índice RAE mede a fragmentação partidária em uma eleição. Isso é feito a partir da quantidade relativa de cadeiras legislativas de cada partido. A participação partidária é uma medida global. O índice considera a participação de cada um dos partidos em um dado sistema eleitoral a partir das cadeiras legislativas conquistadas por estes partidos. Isso significa que o índice RAE mensura o quanto os partidos, dentro de uma média geral, têm de representação política dentro desse universo global.
Isso significa que o índice RAE mensura o quanto todos os partidos, se reduzidos a um único partido, têm de representação política. Teoricamente, um único partido teria 100% de representação política o que equivale dizer que a fragmentação é zero. Na prática, com mais de um partido, a representação de um partido reduz a representação dos outros. Fazendo “uma média” é possível saber o quanto há de representação média se essa realidade fosse convertida para um partido único. Ou seja, o cálculo estima o quanto um partido único teria de representação (força política) se todo o sistema partidário fosse reduzido a esse partido único. A partir do cálculo da representação é possível chegar à fragmentação, já que um valor é complementar ao outro.
Agora vamos analisar a equação. Ela tem duas parcelas. A parcela à esquerda que é o número 1 e a parcela à direita que é a somatória ao quadrado das proporções das cadeiras adquiridas pelos partidos. A segunda parcela representa, em termos matemáticos, para o presente caso, a representação (ou participação) partidária.
Essa ideia, presente na segunda parcela da equação, não é exclusiva da Ciência Política e pode ser vista, por exemplo, na Economia ao avaliar o nível de concorrência de empresas em um mercado, o que é indicado pelo índice Herfindahl. Assim, quando este valor é subtraído de 1 passa a expressar o contrário, ou seja, a “não-participação partidária”. Em outros termos, indica a fragmentação partidária. Um questionamento que pode surgir é por qual motivo se usa (pi)2 e não somente (pi). A resposta para isso é conceitual.
Logo, partimos da ideia que a segunda parcela da equação representa o nível de participação dos partidos. Assim, se usarmos (pi); a resposta resulta, matematicamente incongruente. Caso seja usado (pi)2 teremos, matematicamente, um valor coerente para análise. Os exemplos a seguir explicam o conceito e deixam a ideia clara, a partir de situações homogêneas de distribuição. Importante observar que ainda que pareça que o uso de (pi)2 distorce o resultado, isso não é real, na verdade assim que o resultado faz sentido.
Situação exemplo: Supondo dois partidos, A e B; onde cada qual tem 50% das cadeiras da casa legislativa; qual a participação partidária deste sistema partidário? A partir deste exemplo, se usarmos (pi) teremos: Partido A: 0,5; Partido B: 0,5. Assim, 0,5 + 0,5 = 1. Logo, a partir deste cálculo a participação partidária é 1, ou de 100% o que está errado porque a participação partidária é de 50%; já que são dois partidos e cada qual tem 50% das cadeiras na casa legislativa.
Quando se aplica (pi)2 o cálculo fica da seguinte forma: Partido A: 0,5; Partido B: 0,5. Assim, (0,5)2 + (0,5)2 = 0,25 + 0,25 = 0,5. Logo, a partir deste cálculo a participação partidária é 0,5, ou de 50% o que está em conformidade com a realidade; pois são dois partidos e cada qual tem 50% das cadeiras legislativas.
Isso é replicado para qualquer distribuição homogênea. Ou seja, independentemente do número de partidos e da participação (até então, participação com distribuição homogênea), os resultados serão sempre o mesmo.
Por exemplo; no caso de três partidos onde cada qual tem 33% das cadeiras legislativas; o resultado para (pi) e (pi)2 é, respectivamente; 1 e 0,33; ou, 100% e 33%. Na mesma lógica, para 4 partidos e cada qual com 25% das cadeiras legislativas temos, para (pi) e (pi)2 é, respectivamente; 1 e 0,25; ou, 100% e 25%.
Assim, o cálculo com uso de (pi) será sempre 1 e se usado (pi)2 será sempre 1/(número de partidos). E isso independe de a distribuição ser ou não homogênea. Ela serve para qualquer tipo de distribuição, podendo ser extrapolado para distribuições heterogêneas, estas mais reais.
Logo, o resultado que nos interessa é quando se usa (pi)2 no segundo termo. Desta forma temos uma medida para análise prática.
Interpretação: Os valores limites para o índice RAE é 0 e 1. Quando é 0 (zero) representa a mínima fragmentação partidária possível. Quando é 1 (um) representa a máxima fragmentação partidária possível. Logo, para valores entre 0 e 1 temos os valores reais. Valores baixos do índice RAE representam baixa fragmentação partidária. Já valores altos do índice de RAE representam alta fragmentação partidária.
Dados de Entrada: Para calcular o índice RAE dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice RAE.
Exemplo: Calcular a fragmentação partidária a partir dos dados da Tabela 02. A partir da Tabela 02, temos que o cálculo do índice RAE fica: RAE = 1 – Σp2. Logo; RAE =1 – 0,18587; o que resulta em RAE = 0,8141; ou 81,41%. Então, para o exemplo apresentado, a fragmentação partidária é alta.
3.2: Número Efetivo de Partidos – ENP
Proposição: O índice ENP foi criado em 1979, proposto por Laakso (Markku Laakso; Médico – Finlândia) e Taagepera (Rein Taagepera; Cientista Político e Político – Estônia). O índice mede a fragmentação partidária em um país, como sugere o título e mensura a quantidade de partidos com força real dentro de uma casa legislativa. O valor numérico pode ser dado na forma de índice, com valores entre 0 e 1 ou pode ser apresentado na forma percentual. O primeiro é mais comum.
Equação: A equação 3 calcula o ENP.
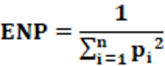
Conceitos: Conceitualmente, é um número que representa a quantidade de partidos que efetivamente tenham poder político em uma casa legislativa e não um índice. Ainda, do ponto de vista conceitual, não mede a fragmentação partidária em um país, ainda que na prática permita essa inferência.
O ENP é usado para avaliar o número efetivo de partidos em um país. Entretanto, se realizadas as devidas adaptações pode ser usado para avaliar uma região qualquer, seja um estado ou um município, por exemplo. Logo, a determinação do ENP ocorre a partir do tamanho relativo de cada partido a partir do número de cadeiras dentro de uma dada casa legislativa. No geral, a casa legislativa adotada é a Câmara dos Deputados Federais e serve, neste formato, para vários fins, entre eles permite comparar Sistemas Partidários entre países, por exemplo.
Interpretação: O ENP indica a quantidade de partidos com força política real em um país. O ENP não tem relação com o número de partidos, mas com o número de partidos que exercem determinada força política dentro da casa legislativa. Ao fim, alguns exemplos vão deixar a ideia mais clara. Assim, mesmas quantidades de partidos, com proporções de cadeiras diferentes entre os partidos altera o valor do ENP. Logo; o ENP mensura a quantidade destes partidos o que significa dizer que a força é vista a partir do poder relativo entre os partidos.
ENP Baixo: Isso ocorre em duas situações: a) quando há poucos partidos; b) quando a distribuição é desproporcional, ou seja, quando poucos partidos ficam com muitas cadeiras legislativas e muitos partidos ficam com poucas cadeiras. Valor de ENP baixo representa que há poucos partidos com força política real ou seja, há um ou poucos partidos dominantes na casa legislativa, em função da distribuição ser mais desproporcional.
ENP Alto: De forma análoga, isso ocorre em duas situações: a) quando há muitos partidos; b) quando a distribuição é mais proporcional, ou seja, quando as cadeiras são divididas de forma mais homogênea entre os partidos. Assim, valor de ENP alto representa que há muitos partidos com força política real ou seja, que não há um ou poucos partidos dominantes, mas que existe um número considerável de partidos com razoável poder na casa legislativa em função de seu tamanho relativo mais homogêneo.
De forma matemática o ENP informa quantos partidos têm poder na casa legislativa para interferir na aprovação, de forma a aprovar ou não proposições legislativas. Resumindo, o ENP representa o número de partidos com força política real em determinada região. A partir do conceito, o ENP pode variar de 1 até, teoricamente, infinito. Quando ENP = 1 temos a presença de um único partido dominante. Para valores diferentes temos a quantidade de partidos dominantes conforme o valor próprio do ENP.
Dados de Entrada: O cálculo neste artigo considera a ideia clássica e utiliza os dados da Câmara dos Deputados Federais. Nesta toada o único dado necessário é a proporção de cadeiras de cada partido na Câmara dos Deputados Federais. Para esse cálculo é necessário saber quantas cadeiras cada partido tem e o número total de cadeiras da casa legislativa. Para isso devemos usar a equação 1. Logo, após algumas poucas manipulações algébricas é obtido o valor ENP – Número Efetivo de Partidos.
Exemplo: A partir da Tabela 2 e da equação 3, temos: ENP vale: ENP = 1/p2 = ENP =1/0,18587; logo ENP = 5,38. Logo, para o exemplo, o número efetivo de partidos é dado por algo em torno de 4 partidos. Se observarmos os três primeiros partidos vemos que eles possuem um número elevado de cadeiras se comparados aos demais.
Alguns exemplos para interpretação do índice: Situação 1: Partido 1: 60 cadeiras; Partido 2: 2 cadeiras. ENP = 1,066. Situação 2: Partido 1: 60 cadeiras; Partido 2: 55 cadeiras. ENP = 1,996. Na situação 1 o ENP é, aproximadamente 1, mesmo com a existência de dois partidos. Na situação 2 há a mesma quantidade de partidos, entretanto, a distribuição de cadeiras é bastante homogênea, resultando em ENP, aproximadamente, 2. A explicação para isso está na distribuição das cadeiras entre os partidos. Logo; neste caso, o fator preponderante é a distribuição das cadeiras entre os partidos.
Situação 3: Partido 1: 60 cadeiras; Partido 2: 55 cadeiras; Partido 3: 42 cadeiras; Partido 4: 12 cadeiras; Partido 5: 9 cadeiras; Partido 6: 8 cadeiras; Partido 7: 6 cadeiras; Partido 8: 3 cadeiras; Partido 9: 2 cadeiras; Partido 10: 1 cadeira. ENP = 4,49. Situação 4: Partido 1: 60 cadeiras; Partido 2: 55 cadeiras; Partido 3: 42 cadeiras; Partido 4: 50 cadeiras; Partido 5: 57 cadeiras; Partido 6: 45 cadeiras; Partido 7: 55 cadeiras; Partido 8: 35 cadeiras; Partido 9: 32 cadeiras; Partido 10: 46 cadeira. ENP = 9,66. Neste caso podemos evidenciar que o ENP tem forte influência da distribuição das cadeiras legislativas entre os partidos. Nas duas situações temos o mesmo número de partidos, no caso,10. Entretanto, como a distribuição das cadeiras na situação 3 é mais desproporcional, o ENP tem valor aproximado da quantidade dos partidos com a maior quantidade de cadeiras. Já na situação 4, como a distribuição das cadeiras é bem mais homogênea, o ENP tem valor quase igual à mesma quantidade de partidos existentes. Por mais uma vez é possível observar que o ENP é função da distribuição das cadeiras na casa legislativa e não da quantidade de partidos.
Situação 5: Partido 1: 60 cadeiras; Partido 2: 55 cadeiras; Partido 3: 42 cadeiras; Partido 4: 12 cadeiras; Partido 5: 9 cadeiras; Partido 6: 8 cadeiras; Partido 7: 6 cadeiras; Partido 8: 3 cadeiras; Partido 9: 2 cadeiras; Partido 10: 1 cadeira; Partido 11: 9 cadeiras; Partido 12: 8 cadeiras; Partido 13: 6 cadeiras; Partido 14: 3 cadeiras; Partido 15: 2 cadeiras; Partido 16: 1. ENP = 5,77. Aqui é possível observar que a quantidade de partidos tem menor influência. A maior influência e sentido para o ENP é o tamanho relativo entre os partidos e o poder que tem, o que é visto através das cadeiras que cada partido tenha na casa legislativa o que é, ao fim, uma medida relativa.
4: Índices de Desvio Linear
São índices que utilizam a diferença absoluta entre a proporção de votos de cada partido e a proporção de assentos conquistados por eles na casa legislativa.
4.1: Índice RAE de Desproporcionalidade do Sistema Eleitoral
Proposição: Como o índice anteriormente apresentado, o RAED foi criado em 1967 e proposto por Rae (Douglas Whiting Rae; Cientista Político – Estados Unidos). O índice RAED mede a desproporcionalidade da representação dos partidos em um sistema eleitoral. Pode ser dado na forma numérica ou na forma percentual. A mais comum é a primeira forma, ainda que a segunda seja mais intuitiva.
Equação: A equação que calcula o índice RAED é apresentada na equação 4.
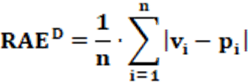
Conceitos: Conceitualmente, o índice RAED mede o desvio médio (e não o desvio total) em uma eleição e serve para verificar o nível de desproporcionalidade quanto à quantidade de cadeiras conquistadas pelos partidos com relação à proporção dos votos recebidos. É o mais antigo índice de desproporcionalidade do sistema eleitoral.
Pela equação é possível notar que o índice RAED é uma média, já que a somatória é dividida pelo número de partidos. Por isso mede o desvio médio. Entretanto, a equação possui um problema de duplicidade de valores. Para entender isso temos que compreender a diferença entre vi – pi. O parâmetro pi indica a proporção de cadeiras conquistadas por um partido qualquer. Já vi indica a proporção de votos que esse partido obteve nas eleições.
Assim, quando vi > pi isso representa que houve maior proporção de votos do que a proporção de cadeiras conquistadas. E como o cálculo é feito a partir de proporções (relativas), as cadeiras que um partido não ganhou fica para outro partido. Portanto, para o partido A; vi – pi = X; então, para um partido B, teremos vi – pi = -X. Entretanto, como o valor é dado em módulo o valor -X acaba se transformando em X; o que faz com que o valor X apareça duas vezes; ou seja, 2X. Por isso há duplicidade de valores.
Isso não significa que o índice não tenha seu valor, já que isso deve ser considerado na análise. Ademais, há índice que elimina essa duplicidade de valores, como veremos neste artigo. O que temos que entender é que o índice RAED é uma média do desvio entre a proporção de cadeiras conquistadas (vi) com a proporção dos votos obtidos (pi). E desta forma permite mensurar o nível de desproporcionalidade de um dado sistema eleitoral.
Algo que devemos entender é que dentro de um pleito eleitoral quando um partido pequeno recebe votação (vi > 0), mas não recebe cadeiras (pi = 0) então o índice RAED é subestimado. Assim, pequenos partidos, com pouca votação e pouca ou nenhuma cadeira conquistada subestima o índice RAED. Um dos elementos que contribui para isso é o número de partidos (n), que passa de n (sem a presença do partido pequeno) para n + 1 (com a presença do partido pequeno).
Interpretação: Para fins de apresentação é mais sugestivo apresentar o valor na sua forma percentual. A ideia de interpretação é simples. Quanto menor o valor calculado, menos desproporcional é o sistema eleitoral. Para valores maiores, maior é desproporcionalidade do sistema eleitoral.
Dados de Entrada: Para calcular o índice RAED dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice RAED.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi | = 0,33757; logo RAED = 33,75%.
4.2: Índice Loosemore–Hanby de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Losemore-Hanby (LH) foi criado em 1971, proposto por Loosemore (John Loosemore) e Hanby (Victor J. Hanby). O índice LH mede a desproporcionalidade da representação dos partidos em um sistema eleitoral.
Seu valor pode ser apresentado na forma numérica, quando calculado a partir das proporções ou pode ser apresentado na forma percentual, quando calculado a partir de valores percentuais. Os dois são utilizados, entretanto, o valor percentual é mais comum.
Equação: A equação que calcula o índice LH é apresentado na equação 5 e lembra bastante a equação para o índice RAED.
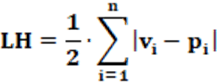
Conceitos: Conceitualmente, o índice LH mede o desvio total (e não o desvio médio) em uma eleição e serve para verificar o nível de desproporcionalidade quanto à quantidade de cadeiras conquistadas pelos partidos com relação à proporção dos votos recebidos. É considerado índice mais real para análise de desproporcionalidade do sistema eleitoral que o índice RAED. Isso devido à medida de desvio total e não do uso médio.
Ele é calculado através da diferença absoluta, em módulo, entre a proporção (ou percentual) de cadeiras conquistadas por esse partido na casa legislativa – (vi) e a proporção (ou percentual) de votos recebidos por um partido (pi). Assim, a partir deste raciocínio, o índice LH permite mensurar o quanto uma eleição desvia-se do princípio eleitoral que diz: “Uma pessoa, um voto”. Em outras palavras o índice LH informa, a respeito dos votos que foram desperdiçados.
Isso porque se vi = pi isso significa que todo voto dado por parte dos eleitores foi convertido em cadeiras na casa legislativa. Quando vi > pi isso significa que a proporção de votos recebidos foi maior que a proporção de cadeiras conquistadas por esse partido. Logo; a diferença entre vi – pi representa a parcela de votos dos eleitores a esse partido que não tiveram relevância alguma para a conquista de cadeiras na casa legislativa. Nesse caso há prejuízo ao partido.
Se vi < pi isso significa que a proporção de votos recebidos foi menor que a proporção de cadeiras conquistadas por esse partido. Ainda que para esse partido a conquista de cadeiras foi melhor que sua votação, isso traz prejuízo para outro partido porque o cálculo é feito a partir de proporção, o que considera o valor total. Portanto; para este último caso, a diferença vi – pi representa a parcela de votos dos eleitores que não votaram nesse partido e que mesmo assim garantiu a esse partido a conquista de cadeiras na casa legislativa. Nesse caso há benefício ao partido.
Portanto; para cada prejuízo a um partido há benefício para outro partido. Isso porque o cálculo considera proporções das cadeiras conquistadas por cada partido (pi). Diante desse raciocínio é possível notar que o resultado vi – pi aparecerá duas vezes; uma na forma de prejuízo ao partido A e outra vez na forma de benefício ao partido B. Por isso, para evitar duplicação dos mesmos valores existe a divisão por 2. Importante destacar que o cálculo é feito utilizando o módulo da diferença entre os valores. Assim, a divisão por 2 é para evitar que a análise seja feita considerando duas vezes o mesmo valor.
Por fim, retomando a ideia anterior, o índice LH, na forma como é calculado por definição, indica a quantidade de votos desperdiçados. Isso é visto quando vi < pi. Logo, o índice LH mede, de fato, a desproporcionalidade de um sistema eleitoral, em determinada eleição. Fala-se em desproporcionalidade e não em proporcionalidade dado seu conceito formal e matemático.
Interpretação: Para fins de apresentação é mais sugestivo apresentar o valor na sua forma percentual. A ideia de interpretação é simples. Quanto menor o valor calculado, menos desproporcional é o sistema eleitoral. Para valores maiores, maior é a desproporcionalidade do sistema eleitoral.
Dados de Entrada: Para calcular o índice LH dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice LH.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi | = 0,33757; logo LH = 16,87%.
4.3: Índice Rose de Proporcionalidade do Sistema Eleitoral
Proposição: O índice ROSE (RO) foi criado em 1984, proposto por Rose (Richard Rose; Cientista Político – Estados Unidos). O índice mede o nível de proporcionalidade da representação dos partidos em um sistema eleitoral de um dado país. O valor numérico pode ser dado na forma de índice, com valores entre 0 e 1, mas é apresentado, geralmente, na forma percentual.
Equação: A equação que calcula o índice RO é apresentado na equação 6.
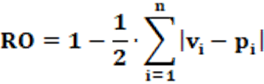
Pode ainda ser expresso conforme equação 7.
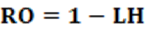
Conceitos: Conceitualmente, o índice RO é complementar ao índice LH. O índice Rose mede o grau de representação dos partidos dentro de um sistema eleitoral, em um dado país. Como LH mede a desproporcionalidade da representação dos partidos no sistema eleitoral, quando este é subtraído de 1, obtermos o contrário complementar que é a proporcionalidade da representação dos partidos no sistema eleitoral. A desproporcionalidade é vista pelo desvio, este dado pela somatória da diferença entre vi e pi. Retirada a desproporcionalidade, o que resta é a proporcionalidade. Ou seja, a proporcionalidade da representação dos partidos dentro do sistema eleitoral.
Interpretação: A interpretação dos valores é direta. Para valores altos do índice RO, há alta proporcionalidade da representação dos partidos políticos no sistema eleitoral. Para valores baixos do índice RO, é indicativo de baixa proporcionalidade da representação dos partidos políticos no sistema eleitoral.
Dados de entrada: Para calcular o índice RO dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice LH. Podemos ainda utilizar como dado de entrada o próprio índice LH.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi | = 0,33757; logo RO = 83,13%.
4.4: Índice Grofman de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Grofman (G) foi proposto em 1985, por Grofman (Bernard Norman Grofman; Cientista Político – Estados Unidos). O índice é também conhecido como índice Loosemore-Hanby ajustado. O índice G mede a desproporcionalidade da representação dos partidos em um sistema eleitoral.
Equação: A equação que calcula o índice G é apresentado na equação 8.
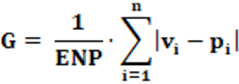
Podemos observar que ENP = 1/(pi)2. Logo; após alguns poucos manejos algébricos, teremos, como resultado, a equação 9.
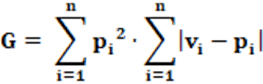
As duas equações são, ao fim, a mesma, o que muda é sua forma de apresentação.
Conceitos: Conceitualmente, o índice G é uma modificação do índice RAED e do índice LH. Com relação ao índice LH, o índice G substitui a divisão por 2 pela divisão por ENP. Enquanto o índice LH, matematicamente, utiliza e mensura o desvio total, o índice G mensura o mesmo desvio ponderado pelo ENP; o que é uma medida da realidade quanto à quantidade efetiva de partidos, ou, de forma indireta, a fragmentação partidária.
Disso resulta uma observação importante. O índice de RAED é calculado a partir do desvio médio, uma vez que o desvio é dividido pelo número de partidos existente. E esta é a diferença quanto ao índice G, já que este é dividido pelo número efetivo de partidos e não pelo número real de partidos. Tudo isso implica que o índice G tem valor intermediário entre o índice RAED e o índice LH. É um índice que utiliza o desvio entre os valores pi e vi. Por se tratar de desvio o valor é absoluto. O que muda, em seu caso, é sua ponderação que é feita através do ENP. Como o índice LH tem ponderação por 2 e o índice RAED tem ponderação N (número de partidos) e, a partir disso podemos afirmar que 2 < ENP < N; o que resulta, obrigatoriamente na seguinte relação: RAED < G < LH.
O fato de utilizar o ENP como ponderação, traz uma visão mais realista. O uso de N (caso do índice RAED) e o uso de 2 (caso do índice LH) como elementos de ponderação não são tão realistas quanto o índice G. Isso porque o ENP reflete, de fato, a força dos partidos e essa força pondera o desvio da representação partidária dos partidos que têm representação significativa, ou, em outras palavras, partidos com relevância e força política.
Assim, o índice G possui caráter mais realista que os índices RAED e LH pelo simples fato de o índice G ponderar seu valor de desvio usando uma medida de valor real que é o ENP. Uma observação interessante é que o índice RAED e o índice G podem apresentar valores diferentes para os mesmos desvios porque os denominadores variam conforme o caso, respectivamente N e ENP. Já, no caso do índice LH, para mesmos desvios, o valor será sempre o mesmo, porque o denominador é o mesmo (2), recordando que ele é calculado a partir do desvio total.
Por fim, o índice G, tem o desvio absoluto dividido igualmente entre todos os partidos efetivos do cenário político. Por isso possui caráter mais realista. O valor final indica o nível de desproporcionalidade absoluta |(vi – pi)| com relação ao quanto isso afeta cada um dos partidos efetivos (ENP), uma forma de distribuição da desproporcionalidade aos partidos efetivos.
Interpretação: A interpretação dos valores é direta. Para valores baixos do índice G, há baixa desproporcionalidade da representação dos partidos políticos no sistema eleitoral. Para valores altos do índice G, é indicativo de alta desproporcionalidade da representação dos partidos políticos no sistema eleitoral.
Dados de entrada: Para calcular o índice G dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice G.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi | = 0,33757; e sendo ENP = 5,38; logo G = 6,27%.
5: Índices de Desvio Quadrático
São índices que utilizam a diferença absoluta entre a proporção de votos de cada partido e a proporção de assentos conquistados por eles na casa legislativa. A diferença é elevada ao quadrado.
5.1: Índice Gallagher de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Gallagher (LSq) foi criado em 1989, e apresentado publicamente em 1991. Foi proposto por Gallagher (Michael Gallagher; Cientista Político – Reino Unido). O índice mede o nível de desproporcionalidade da representação dos partidos em um sistema eleitoral de um dado país. O valor numérico é dado na forma de índice, com valores entre 0 e 100.
Equação: A equação que calcula o índice LSq é apresentada na equação 10.
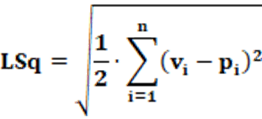
Conceitos: O índice Gallagher é usado como referência para comparação entre países e é representado como LSq porque faz alusão ao termo Least Square. Entretanto, do ponto de vista matemático, o nome está inadequado, uma vez que não há nenhuma minimização dos quadrados. O uso de LSq para representar o índice é feito por questões de um reconhecimento já difundido e não por questões conceituais. Por isso, por vezes, alguns autores no lugar de usar LSq usam “G” para indicar o índice. Conceitualmente, o índice LSq parte da soma dos resíduos ao quadrado. Resíduo, conceitualmente é a diferença entre um valor ideal e um valor real ou previsto.
Assim, vi representa o valor ideal e pi o valor real. A diferença entre vi e pi é o resíduo. Essa diferença é feita para cada partido i. O resíduo é elevado ao quadrado porque se em um dado partido A vi – pi = X, para o partido B vi – pi = -X. Isso porque o cálculo considera as proporções de votos (vi) e as proporções de cadeiras obtidas na casa legislativa (pi). Logo, se o partido A tem uma variação positiva, resultando X; isso deverá ser compensado, fazendo com que o partido B tenha, como resultado, -X.
Portanto; se o cálculo não é feito a partir do módulo ou se ele não é elevado ao quadrado (ou outro expoente par), o resultado da somatória será zero. Logo, sem o uso do módulo, uma forma para que a somatória não resulte em zero é o uso de um expoente par, no caso o 2; ou seja, o uso do quadrado. Por isso o cálculo é feito, conceitualmente, a partir da soma do quadrado dos resíduos. A raiz quadrada é utilizada para retornar à dimensão original, transformando o resíduo ao quadrado em apenas resíduo. A divisão por 2 altera a escala do índice LSq fazendo um ajuste de forma que o resultado seja fiel aos dados.
Por exemplo. Supondo um caso de dois partidos, A e B; onde o partido A tem 100% dos votos e o partido B tem 0%. Por alguma manobra política o partido A fica sem nenhuma cadeira na casa legislativa e o partido B ganha todas. Nesta situação, para o partido A, o resíduo é 100 – 0; o que resulta em 100. Para o partido B, o resíduo é 0 – 100; o que resulta em -100. Elevando cada um destes valores ao quadrado, se obtém 10.000, tanto para o partido A como para o partido B. A soma; portanto, resulta em 20.000, que ao ser dividido por 2, volta ao valor 10.000; cuja raiz quadrada é 100. Logo a desproporcionalidade da representação partidária neste sistema eleitoral é de 100%.
Logo, se não houvesse a divisão por 2, o resultado seria 70,71%. Logicamente, esse valor não condiz com os dados do nosso exemplo. Portanto; a divisão por 2 é um acerto do cálculo. Devemos recordar que o cálculo, quando tratamos da diferença entre proporções, ocorre sempre duas vezes. Logo, a divisão por 2 não é fruto do acaso. Em termos de sensibilidade pequenas alterações, provocadas por partidos pequenos, é o que apresenta maior sensibilidade. Logo, confere uma boa leitura quanto à desproporcionalidade da representação partidária em um dado sistema eleitoral.
Interpretação: Ainda que o índice seja apresentado, comumente, por um valor numérico, ele pode facilmente ser interpretado como se fosse percentual. Isso ocorre porque o índice tem valores entre 0 e 100. Para um índice 0, temos o caso ideal de representação, sem nenhuma desproporcionalidade da representação partidária no sistema eleitoral. No caso de um índice 100, isso representa a maior distorção, ou seja, a maior desproporcionalidade da representação partidária no sistema eleitoral. Para valores entre 0 e 100; a interpretação é direta. Quanto maior o índice, maior é a desproporcionalidade da representação partidária no sistema eleitoral.
Dados de entrada: Para calcular o índice LSq dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice LSq.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi |2 = 0,03770; logo LSq = 13,72%.
5.2: Índice de Sainte-Lagüe de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Sainte-Lagüe (SL) é baseado nos estudos do matemático francês André Sainte-Lagüe. Foi criado por Gallagher, o mesmo do índice Gallagher – LSq. O índice mede o nível de desproporcionalidade da representação dos partidos em um sistema eleitoral de um dado país. O valor numérico é dado na forma percentual, bem como os valores utilizados para o cálculo, que no lugar dos valores proporcionais, até então empregados, usa valores já na forma percentual.
Equação: A equação que calcula o índice SL é apresentado na equação 11.
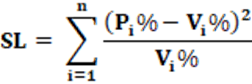
Conceitos: O índice Sanite-Lagüe tem o formato da distribuição de probabilidade Qui-Quadrado. Neste formato, temos a diferença entre o valor observado Oi; e o valor esperado Ei. Esta diferença é elevada ao quadrado e dividida pelo valor esperado Ei. No nosso caso, Pi% faz o mesmo papel de Oi e Vi% faz o mesmo papel de Ei.
A equação apresenta a soma dos resíduos ao quadrado, semelhante ao índice LSq. Entretanto, no lugar de realizar a divisão por 2 e extrair a raiz, para voltar à mesma dimensão; é realizada a ponderação, que é a divisão por Vi%. Essa ponderação permite distribuir o valor dos resíduos para cada um dos votos recebidos pelo partido i. Representa o peso que cada partido tem de votação (Vi) na votação total V. Ou seja, o índice SL calcula a proporção de votos perdidos (que não foram convertidos em cadeiras na casa legislativa) ou de votos ganhos além de sua própria votação (cadeiras na casa legislativa conquistadas sem a votação correspondente) distribuídos para cada eleitor, que é o valor esperado, conforme o princípio eleitoral “Uma pessoa, um voto”, conforme descrito no índice LH.
Em suma, o índice SL mede a dispersão dos resíduos (diferença entre o esperado e o real) para o universo dos eleitores votantes no partido i. Entenda-se entre esperado e real, respectivamente, como Vi% e Pi%. O teste do Qui-Quadrado, assim como o índice SL tem por finalidade comparar proporções (em nosso caso Vi% e Pi%) e estimar o nível de divergência existente entre o valor esperado Vi% e o valor real Pi%.
Como o índice SL tem a divisão por Vi%; isso representa que as maiores votações Vi apresentam maior dispersão do quadrado dos resíduos (ou desvio relativo) por eleitor; minimizando o índice SL. No caso de Vi ter valores baixos, ocorre o contrário, ou seja, a dispersão dos desvios relativos, por eleitor, é maximizada; aumentando o índice SL. Obviamente que o valor do desvio também deve ser considerado, principalmente porque ele é elevado ao quadrado. Logo, a diferença absoluta entre Vi% e Pi% influencia fortemente o índice. Mas mesmo assim, ainda com valores altos de desvio relativo (resíduos) o quociente é capaz de minimizar a desproporcionalidade. Logo, existe um balanço que é visto exatamente pela ponderação, dado pelo quociente do índice SL.
Por fim, para resultados possíveis, não devemos usar partidos que não tiveram votação, ou seja, partidos com Vi = 0. Isso porque 1/Vi vai ao infinito e isso leva SL ao infinito. Se aplicado o limite nesse ponto, verifica-se que ele não existe porque os valores no lado esquerdo e direito são diferentes, o que torna o limite inexistente, conforme equação 12 e resolução na sequência.
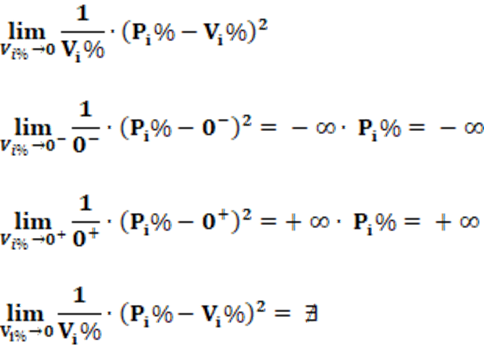
Interpretação: A interpretação do índice SL é direta e dada em termos percentuais. Para valores baixos, temos menor desproporcionalidade da representação partidária no sistema eleitoral. Para valores altos do índice SL, a desproporcionalidade da representação partidária no sistema eleitoral é igualmente alta. Os valores do índice SL variam de 0 até infinito; o que incorre em aparente incongruência, ainda que isso se dê em um caso extremo. Os valores acima de 100 são bastante comuns. O valor infinito aparece quando um partido qualquer, sem nenhuma votação (Vi = 0); ganha alguma cadeira. Isso faz com que 1/Vi vá ao infinito, porque, neste caso, Vi = 0.
Dados de entrada: Para calcular o índice SL dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido, em termos percentuais (Vi%). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido em termos percentuais (Pi%). Assim, a partir de Vi% e Pi% é calculado o índice SL.
Exemplo: A partir da Tabela 3 temos o valor direto do índice SL; pois SL = Σ( | Vi%- Pi% |2/Vi%)= 2,1724; logo SL = 217,24%.
5.3: Índice Monroe de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Monroe (MO) foi criado em 1994. Foi proposto por Monroe (Burt L. Monroe; Professor de Ciência Política – Estados Unidos). O índice mede o nível de desproporcionalidade da representação dos partidos em um sistema eleitoral de um dado país. O valor numérico é dado na forma de índice, com valores entre 0 e 100.
Equação: A equação que calcula o índice MO é apresentado na equação 13.
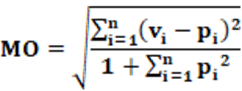
Conceitos: Conceitualmente, o índice MO parte da soma dos resíduos ao quadrado. Como visto no índice LSq, resíduo, conceitualmente, é a diferença entre um valor ideal e um valor real ou previsto. No caso do índice Lsq o denominador é “2”. No caso do índice MO, o denominador é “1 + Σ(pi)2“. Para fins de análise é conveniente realizar alguns manejos algébricos. O primeiro a fazer é considerar que Σ(pi)2 = 1/ENP. Após essa substituição e alguns manejos algébricos a equação 13 é transformada na equação 14.
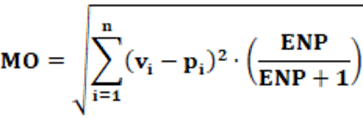
Isso resulta que o índice MO é alterado conforme cada situação, já que o valor ENP é diferente para cada caso. Isso confere uma vantagem com relação ao índice LSq, uma vez que esse último índice não se altera conforme o caso porque o denominador é fixo, no caso, 2. Ao contrário, o índice MO, tem uma correção a cada caso já que utiliza como meio de correção o ENP. É possível observar que o fator de correção (ENP/(ENP+1)) sempre resultará em valor menor que 1, ou seja, (ENP/(ENP+1)) < 1 porque o numerador é menor que o denominador.
Outros manejos algébricos permite estimar o índice MO a partir do índice LSq. A equação 15 mostra essa relação.
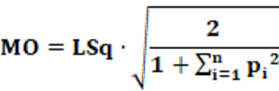
À exceção do fator de correção, tudo o que é válido, conceitualmente, para o índice LSq é válido par o índice MO. Portanto; a ideia se mantém. Uma observação interessante, é que para o caso particular de ENP = 1; o valor do índice MO é o mesmo do índice LSq. Uma segunda observação é que para qualquer valor de ENP diferente de 1, o índice MO será sempre maior que o índice LSq. Isso ocorre porque o fator multiplicativo do índice LSq é 0,5 (= 1/2) e para o índice MO será maior que 0,5, para o caso de ENP > 1. Ademais, quanto maior o ENP, maior será o fator de correção (fator multiplicativo), de forma que se ENP → ∞ o fator de correção tenderá a 1.
Por fim, a equação 15 pode ser reescrita conforme a equação 16.
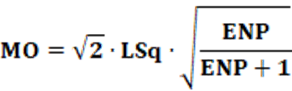
Interpretação: O índice é apresentado através de um valor numérico. Quanto maior o valor do índice maior é a distorção, ou seja, a maior desproporcionalidade da representação partidária no sistema eleitoral. Para valores baixos do índice, de forma análoga, menor será a desproporcionalidade da representação partidária no sistema eleitoral. Logo, como a maioria dos índices, a interpretação é direta. Por fim, a equação 16 mostra, matematicamente, que para ENP > 1; o índice MO será sempre maior que o índice LSq.
Dados de entrada: Para calcular o índice MO dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (Vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido (Pi). Assim, a partir de Vi e Pi é calculado vi e pi, respectivamente. Por estes valores determina-se o índice MO.
Exemplo: A partir da Tabela 2, temos Σ| vi – pi |2 = 0,03770; e sendo ENP = 5,38; com uso da equação 14, temos MO = 17,83%.
6: Índices de Valores sobrerrepresentados
São índices que consideram a maior diferença absoluta entre proporção de votos de cada partido e a proporção de assentos conquistados por eles na casa legislativa.
6.1: Índice de Desvio Máximo de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice de Desvio Máximo (MD) é um índice citado em uma das obras de Lijphart no ano de 1994. O índice mede o nível de desproporcionalidade da representação dos partidos em um sistema eleitoral de um dado país a partir da diferença absoluta (e não relativa) entre a proporção de cadeiras obtidas por um partido e a proporção de votos desse mesmo partido. A escolha do partido é feita a partir do valor que fornece a maior diferença entre pi e vi.
Equação: A equação que calcula o índice MD é apresentada na equação 17.
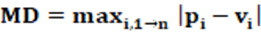
Conceitos: O índice MD caracteriza a desproporcionalidade da representação partidária do sistema eleitoral através do valor de maior desproporcionalidade. Assim, ele utiliza a maior diferença absoluta entre a proporção do número de cadeiras na casa legislativa (pi) e a proporção do número de votos que o partido recebeu (vi). A medida é de simples obtenção, de cálculo rápido e permite uma visão razoável da desproporcionalidade existente. É importante notar que a maior diferença entre a proporção pi e vi, não necessariamente será do maior partido. Pode acontecer, e é bastante comum, que a maior diferença ocorra para o segundo ou terceiro maior partido. Logo, deve estar claro que não se trata de utilizar os dados do maior partido, e sim, de considerar os valores do partido com maior diferença absoluta entre pi e vi.
Interpretação: A interpretação do índice MD ocorre com leitura direta. Para valores pequenos, a desproporcionalidade da representação partidária é baixa. Caso os valores sejam altos, a desproporcionalidade da representação partidária é alta. Os valores vão de 0 até 1. Será 1 quando um partido que não recebeu nenhum voto conquistou todas as cadeiras.
Dados de entrada: Para calcular o índice MD dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido em termos percentuais (pi). Pela comparação da diferença entre todos os valores obtidos para cada um dos partidos, determina-se o índice MD.
Exemplo: A partir da Tabela 2, temos que o maior valor absoluto |vi-pi|, corresponde ao partido 3 e vale 0,18222; o que faz MD = 18,22%.
6.2: Índice Lijphart de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice Lijphart (LJ) foi criado em 1994, proposto por Lijphart (Arend D’Engremont Lijphart; Cientista Político – Países Baixos). O índice mede a desproporcionalidade da representação partidária em um sistema eleitoral. O valor do índice é dado na forma numérica, não na forma percentual.
Equação: A equação que calcula o índice LJ é apresentada na equação 18.
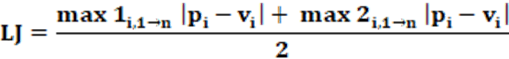
Conceitos: O índice Lijiphart (LJ) caracteriza a desproporcionalidade da representação partidária do sistema eleitoral e é calculado pela média aritmética dos dois valores com maior desproporcionalidade. Essa é calculada através da diferença entre a diferença absoluta da proporção do número de cadeiras na casa legislativa (pi) e a proporção do número de votos que o partido recebeu (vi). A medida, tal como o índice anterior, é de simples obtenção, de cálculo rápido e permite uma visão razoável da desproporcionalidade existente. Visão esta mais aguçada que o índice anterior MD. É importante também notar que as duas maiores diferenças entre a proporção pi e vi, não necessariamente serão dos dois maiores partidos. Os valores a serem usados devem ser norteados pelas maiores diferenças e não com relação ao tamanho dos partidos, ou seja, a quantidade dos votos recebidos ou a quantidade das cadeiras conquistadas.
Uma análise interessante é que o índice LJ é um caso particular do índice de desproporcionalidade de RAED. No lugar de usar “n” como quociente é usado “2”. A proporção do quociente é a mesma porque no caso do índice RAED a média aritmética é feita a partir dos “n” elementos, por isso esse é o denominador. No caso do índice LJ, como a média é feita a partir de dois elementos, o denominador é “2”. A ideia é a mesma, o que muda é a quantidade de elementos utilizados.
Interpretação: A interpretação do índice LJ ocorre, tal como o índice anterior, com leitura direta. Para valores pequenos, a desproporcionalidade da representação partidária é baixa. Caso os valores sejam altos, a desproporcionalidade da representação partidária é alta. Os valores vão de 0 até 1.
Dados de entrada: Para calcular o índice LJ dois dados são necessários: O primeiro dado necessário é a quantidade de votos obtidos por cada partido (vi). O segundo dado necessário é a quantidade de cadeiras obtidas por cada partido em termos percentuais (pi). Pela comparação entre todos os valores obtidos para os partidos, determina-se o índice LJ.
Exemplo: A partir da Tabela 2, temos que o maior valor absoluto |vi-pi|, corresponde ao partido 3 e vale 0,18222; já o segundo maior valor absoluto |vi-pi|, corresponde ao partido 6 e vale 0,05294; o que faz LJ = 0,1175, ou, na forma percentual (não convencioonal), 11,75%.
6.3: Índice D’Hont de Desproporcionalidade do Sistema Eleitoral
Proposição: O índice D’Hont é baseado nos estudos de D’Hont (Victor Joseph Auguste D’Hondt; Advogado de direito civil – Bélgica). O índice mede a desproporcionalidade da representação partidária em um sistema eleitoral. A ideia do índice é manter o menor valor possível para a sobrerrepresentação do partido mais sobrerrepresentado.
Equação: A equação que calcula o índice DH é apresentada na equação 19.
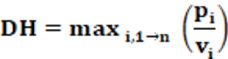
Conceitos: O índice D’Hondt (DH) indica a desproporcionalidade da representação partidária através do quociente entre a a proporção do número de cadeiras na casa legislativa (pi) e a proporção do número de votos que o partido recebeu (vi) a partir do partido mais sobrerrepresentado; ou seja, o que ocorre quando |(pi – vi)| = max< |(pi – vi)| >. Logo, ainda que não seja calculado o índice de de Desvio Máximo (MD) ele é necessário para indicar qual o partido tem a maior sobrerrepresentação. No geral, isso ocorre com partidos maiores. Entretanto, se a sobrerrepresentação ocorrer com partidos menores, o índice tem análise não realista porque resulta em índice com valor maior que de fato é.
O índice D’Hondt mede a discrepância nos valores do partido mais sobrerrepresentado. Logo, para o cálculo do índice D’Hondt sempre deveremos ter pi > vi. Logo, nestas condições pi/vi; > 1. Em um caso ideal, onde pi = vi, teremos, por consequência, pi/vi; = 1. Assim, o intervalo de existência do índice D’Hondt é de 1 até infinito. O valor 1 é para um caso ideal. Já o valor infinito é quando um partido que não recebeu nenhum voto conquistou ao menos uma cadeira na casa legislativa. É infinito porque vi = 0; o que leva pi/vi ao infinito. Neste caso, o índice dá um valor anômalo e no caso de uma sobrerrepresentação de um partido pequeno, o valor é irreal.
Mesmo assim, mesmo com estas exceções, no geral, o índice D’Hont possui boa indicação. O único que se deve ter é atenção quanto aos casos de exceção o que ocorre quando a sobrerrepresentação se der com partidos pequenos. Uma solução que pode ser aplicada, neste casos, é impor uma linha de corte de 5 a 10% a partir dos valores de pi ou vi; conforme o caso ou o método a ser aplicado e entendido pelo analista. A grande vantagem do índice DH é sua facilidade de ser calculado e a boa indicação da desproporcionalidade em casos gerais, que não inclui os casos de exceção. Ademais, ele mantém ao mínimo a sobrerrepresentação do partido mais sobrerrepresentado, não criando valores altos que podem alterar a realidade quando realizada uma análise.
Interpretação: A interpretação do índice DH ocorre a partir da leitura direta do índice. Valores próximos a 1 resultam em baixa desproporcionalidade da representação partidária no sistema partidário. Quanto mais distante de 1, maior a desproporcionalidade. Valores acima de 1.000 ou 2.000 são comuns para esse índice no caso de desproporcionalidade alta no sistema eleitoral.
Dados de entrada: Para calcular o índice DH dois dados são necessários: O primeiro dado necessário é a proporção de votos obtidos por cada partido (vi). O segundo dado necessário é a proporção de cadeiras obtidas por cada partido (pi). Pela comparação entre todos os valores obtidos para os partidos, determina-se o índice DH.
Exemplo: A partir da Tabela 2, temos que o maior valor absoluto |vi-pi|, corresponde ao partido 3 e vale 0,18222; logo, vi = 0,2040 e pi = 0,2222; o que resulta no valor de DH = 1,089.
7: Medidas de Valores de Sobra
São índices que consideram os votos que não são utilizados em uma eleição por questões de origem técnica.
7.1: Voto Desperdiçado
Proposição: Voto desperdiçado foi proposto em 2015 por Stephanopoulos (Nicholas Stephanopoulos; Advogado – Estados Unidos) e McGhee (Eric McGhee; Cientista Político – Estados Unidos). Não é a ideia principal, apenas parte de uma ideia que permite realizar o cálculo da Lacuna de Eficiência.
Equação: A equação que calcula o índice W é apresentada na equação 20.
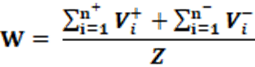
Conceitos: Conceitualmente, voto desperdiçado (W) é todo voto que não gera representação. Dessa premissa surgem dois tipos de votos desperdiçados. O voto excedente (V+) que é a quantidade de votos que ultrapassam o valor necessário para que o partido ou candidato conquiste a cadeira na casa legislativa. Há ainda o voto perdido (V–) que é o voto dado ao partido ou candidato que não conquistou a cadeira na casa legislativa. A soma destes votos é o voto desperdiçado. Portanto; da relação entre o número de votos desperdiçados e o número de votos totais é obtida relação que, apresentada na forma percentual, representa o voto desperdiçado. Desta forma é possível mensurar a quantidade de votos que foram convertidos em representação e quantos votos foram desperdiçados.
Interpretação: A interpretação do índice W é direta. Quanto maior o percentual, maior é a quantidade de votos desperdiçados. Os valores médios são em torno de 50%.
Dados de entrada: Para calcular o índice W é necessário somente saber os votos de cada partido ou candidato, conforme o caso, e disso é possível calcular a quantidade total de votos e selecionar os votos excedentes (V+) e os votos perdidos (V–). Por estes dados calcula-se o índice W.
Exemplo 1: Considerar os dados da Tabela 4, eleição 1 para uma eleição majoritária. Como a eleição é do tipo majoritária, o candidato A conquista a vaga e todos os outros candidatos têm seus votos perdidos. Assim, o valor de (V–) considera os votos dos candidatos B, C, D e E; o que resulta 39.900.000 votos; ou seja V– = 39.900.000. Com relação ao candidato A; ele teria conseguido a cadeira com 31.000.001 votos; logo, a diferença deste com relação a 60.000.000 são os votos excedentes de A, ou seja; V+ = 28.999.999 votos. O total de votos nesta eleição é 100.000.000; disso resulta o número de votos desperdiçados W, que vale 68.899.999 (= 39.900.000 + 28.999.999); que resulta 68,89%.
Exemplo 2: Considerar os dados da Tabela 4, eleição 2 para uma eleição proporcional de 2 cadeiras, com distribuição a partir do método D’Hont. Para o candidato A; pelo método D’Hont, considerando 2 cadeiras, temos a sequência: 60.000.000, 30.000.000, 15.000.000. Para o candidato B, temos, 31.000.000, 15.500.000, 7.750.000. Para o candidato C, temos, 7.000.000, 3.500.000, 1.750.000. Assim, a primeira cadeira é obtida pelo candidato A, pelo valor de 60.000.000 na primeira rodada de distribuição de cadeiras e a segunda cadeira é obtida pelo candidato B pelo valor de 31.000.000. Portanto; o candidato C não obteve cadeira. Logo, a quantidade de votos perdidos é a quantidade de votos do candidato C, ou seja, V– = 7.000.000 votos. Agora devemos calcular os votos excedentes de A e de B. Para A, temos 60.000.000/7.000.000, que resulta 8,57. Usando a unidade, temos 8, que multiplicado por 7.000.000 e acrescido de 1 resulta 56.000.001 votos. Este valor subtraído de 60.000.000 são os votos excedentes do candidato A, que resulta 3.999.999. O mesmo resultado pode ser obtido da seguinte forma: 8,57 – 8 = 0,57. Este valor multiplicado por 7.000.000, resulta 3.999.999,9998. Utilizando a parcela inteira, temos os mesmos 3.999.999. Para o candidato B, os votos excedentes seguem a mesma ideia, 31.000.000/7.000.000, que resulta 4,42, que ao usar a parte inteira, resulta 4, multiplicado por 7.000.000 e acrescido de 1, resulta 28.000.001 votos. Este valor subtraído de 31.000.000 resulta nos votos excedentes de B e vale 2.999.999 votos. Assim, da soma dos votos excedentes de A e B temos V+ = 6.999.998. Logo, o valor W, para este caso, vale 13.999.998 ( = 7.000 .000+ 6.999.998); que resulta 14,28%.
7.2: Lacuna de Eficiência
Proposição: Igualmente proposto por Stephanopoulos (Nicholas Stephanopoulos; Advogado – Estados Unidos) e McGhee (Eric McGhee; Cientista Político – Estados Unidos), no ano de 2015. Esta é a ideia principal, a qual necessita dos valores dos votos desperdiçados (W) para ser calculado. O índice é dado, geralmente, na forma percentual, mas pode ser apresentado na forma numérica (proporção). Ele indica o quão justa é uma eleição distrital e, por inferência, o quanto a manipulação permitiu modificar os resultados de uma eleição se esta fosse realizada de forma justa. É usada para sistemas bipartidários com aplicação de análise do gerrymandering.
Equação: A equação que calcula o índice GAP é apresentado na equação 21.
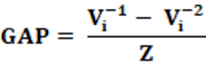
Conceitos: A análise do GAP permite identificar os votos desperdiçados de cada partido, em especial, dos dois maiores partidos e analisa se um deles obteve vantagem na conversão de votos para cadeiras na casa legislativa. Com uso preferível para o voto distrital, o GAP permite apontar qual partido foi beneficiado e qual foi prejudicado. O índice foi, temporalmente, recém construído e tem ainda pouco estudo sobre ele, sua eficiência e resultados. Para fins de construção e interpretação, é interessante manter como (Vi)-1 o partido que recebeu a maior votação total e (Vi)-2 o partido que recebeu a segunda maior votação. Assim, a interpretação passa a ter uma constante para análise.
Interpretação: A interpretação do índice GAP é direta, entretanto há que avaliar o sinal do GAP. A partir da construção indicada, se o GAP é positivo, então a eleição beneficiou o partido com a segunda maior votação. Caso o valor seja negativo isso indica que a eleição beneficiou o partido com maior votação. Independentemente do sinal, o valor absoluto indica, de forma direta, o tamanho da distorção e o quão justa é a eleição, ou ainda, o quão ela se afasta de uma eleição considerada justa.
Dados de entrada: Para calcular o GAP é necessário somente um dado, e é a quantidade de votos obtidos por cada partido, em termos percentuais (Vi%). Deste universo são usados os votos totais e os votos dos dois maiores partidos.
Exemplo 1: A partir dos dados da Tabela 4, considerando que no lugar de candidatos temos partidos, e os cálculos já efetuados no item anterior, temos, para a eleição 1, (Vi)-1 = 28.999.999 e (Vi)-2 = 31.000.000; com uma votação de 100.000.000 votos, temos GAP = 59,99%.
Exemplo 2: A partir dos dados da Tabela 4, considerando que no lugar de candidatos temos partidos, e os cálculos já efetuados no item anterior, temos, para a eleição 2, (Vi)-1 = 3.999.999 e (Vi)-2 = 2.999.999; com uma votação de 98.000.000 votos, temos GAP = 7,14%.
8: Índices de Mobilidade Eleitoral
São índices que mensuram a movimentação dos partidos e a estabilidade destes no sistema eleitoral e partidário, o que considera variações ao longo da linha do tempo.
8.1: Índice Pedersen de Volatilidade Eleitoral
Proposição: O índice Pedersen (P) foi criado em 1979 por Pedersen (Mogens Jin Pedersen; Cientista Político – Dinamarca). O índice mede a volatilidade eleitoral, ou seja, indica a mudança líquida que ocorre no sistema eleitoral de uma eleição t-1 para uma eleição t. Isso é visto através da mudança de voto por parte do eleitor, mudança esta chamada de transferência individual de voto. A mudança global é a somatória da mudança individual.
Equação: A equação que calcula o índice P é apresentado na equação 22.
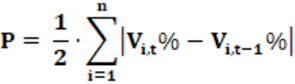
Conceitos: O índice P tem, matematicamente, o mesmo formato que o índice LH. Ou seja, ele é calculado a partir do desvio total. Considera valores absolutos e, por isso, por consequência, um percentual X perdido entre duas eleições pelo partido A, será ganho o mesmo percentual pelo partido B. Disso resulta que |Vi,t% – Vi,t-1%| aparecerá duas vezes, uma como -X (partido A) e outra como +X (partido B). Como são valores absolutos os dois valores entram na somatória como X, o que resulta em 2X. Como existe a divisão por 2; ao fim, o valor resultante será X.
Portanto, toda a ideia conceitual matemática do índice LH pode ser aplicada ao índice P. A diferença entre os índices está na sua construção ideológica. O índice P utiliza a diferença de votos, na forma percentual entre duas eleições, não necessariamente eleições consecutivas. Assim o índice P mede a mudança de votos que os eleitores impõem aos partidos entre duas eleições. Muitas inferências podem ser feitas a partir deste índice, em especial, se avaliada a transferência de votos entre partidos, considerando quem ganhou e quem perdeu, e ainda mais, quanto foi ganho e perdido. Desta forma é possível medir a satisfação e insatisfação por parte do eleitor. Assim a volatilidade eleitoral indica a mobilização de intenção do eleitor e imprime isso na forma percentual.
Interpretação: A interpretação do índice P é direta, através do próprio valor percentual do índice. Quanto maior o valor percentual maiores as mudanças, ou, em termos técnicos, maior é a transferência de votos. Neste caso há indicação de mudança significativa na representação política. Valores baixos indicam menores transferências de votos. Neste caso não houve mudança significativa quanto à representação. Por fim, o nível de contentamento ou descontentamento, inferido pelo índice P, sugere o nível de instabilidade política em determinado país. O descontentamento é visto pela tentativa de mudança, o que indica um índice P alto. Sociedades satisfeitas com sua representação não encontram sentido na mudança de sua representação; o que resulta em um índice P baixo.
Dados de entrada: Para calcular o índice P é necessário somente um dado, e é a quantidade de votos obtidos por cada partido, em termos percentuais (Vi%). Entretanto, este valor deve ser obtido em dois momentos distintos, para duas eleições em momentos diferentes, não necessariamente eleições consecutivas. Assim, a partir de Vi,t% e Vi, t-1% é calculado o índice P.
Exemplo: A partir da Tabela 5, podemos calcular o índice P para vários momentos. Vamos calcular o índice P entre as eleições 9 (ano 2016) e 10 (ano 2020). Assim, a diferença percentual para cada partido é: Partido A = 3,6%; Partido B = 8%; Partido C = 2,6%; Partido D = 1,2%; Partido E = 0,6%. Assim, entre as eleições 2020/2026, o índice P = 8%.
8.2: Índice Lewis de Estabilização Partidária
Proposição: O índice Lewis de estabilização partidária (LW) foi criado em 1994 por Lewis (Paul G. Lewis; Cientista Político). O índice mede a estabilidade dos partidos no cenário político, a partir da permanência deste na arena política ao longo da linha do tempo.
Conceitos: O índice LW mensura o sucesso eleitoral de cada partido ao longo da linha do tempo considerando os resultados de várias eleições. Quanto mais um partido permaneça no cenário político maior é seu sucesso, o que é feito através da aplicação de pesos (recompensas) à proporção relativa de votos obtidos. Estes pesos (recompensas) são crescentes a cada novo pleito. Logo, a manutenção de um partido representa a estabilização deste partido e ao considerar a estabilização de todos os partidos, nós temos a estabilização partidária do sistema eleitoral, uma leitura global. O índice LW é calculado para cada eleição e muda conforme a eleição. Assim, ao longo da linha do tempo é possível obter uma medida quanto à estabilização partidária dentro do sistema eleitoral.
O cálculo é ponderado a partir do conceito de pontuação nocional que é a soma do peso na forma percentual ao longo das eleições. Para a primeira análise (primeira eleição) na linha do tempo, a pontuação nocional adquire valor 100 e o peso vale zero. Na segunda análise (segunda eleição) o peso vale 20% (0,2) e a pontuação nocional é 100% mais 120% (= 100 +20), ou seja, 220%. Na terceira análise (terceira eleição) o peso vale 40% (0,4) e a pontuação nocional vale 220% mais 140% (= 100 + 40), ou seja, 360%. Desta forma o valor atual é ponderado pela soma da pontuação nocional dos histórico analisado.
Assim, é feita a ponderação. Ademais, o peso é aplicado conforme ingresso do partido na arena política. Para a primeira participação do partido, a análise considera que o peso atribuído à votação do partido sempre será zero, mesmo que a análise já exista para anos anteriores. Ou seja, o peso recompensa não só a permanência do partido, mas também sua existência e origem temporal. Se a análise começou no ano X, e tem dois partidos (A e B), nesse ano o peso para os dois partidos é zero. Para o ano X+4; com entrada de um terceiro partido (C), o peso para os partidos A e B será 0,2 (1,2 no total) e o partido C terá peso zero. Já para o ano X+8; termos peso 0,4 (1,4 no total) para os partidos A e B e peso 0,2 (1,2 no total) para o partido C.
Desta forma é feita a atribuição de pesos para os partidos os quais incidem sobre a proporção percentual de votos destes. Importante destacar que os pesos são feitos a partir das eleições em sequência, não dependendo da quantidade de anos entre elas. A medida é a partir das eleições. A medida do índice LW utiliza o peso padrão de 20%. Para o cálculo do índice LW devemos considerar além da pontuação nocional a soma histórica dos índices LW, que é denominada pontuação nominal ponderada. Este último deve ser dividido pelo primeiro e o resultado é multiplicado por 100. O resultado é dado na forma percentual. Uma observação importante é que tanto a pontuação nocional quanto o índice LW, ambos usam valores históricos para calcular o LW do ano em análise.
Interpretação: O índice LW é lido de forma direta. Quanto maior o valor e mais próximo de 100, maior é a manutenção do sistema partidário ao longo do tempo. O aumento do índice entre eleições significa constância no sistema partidário, ou ainda que este não teve alterações, mantendo-se incólume. Caso o índice diminua, significa alterações no sistema partidário.
Dados de Entrada: Para o cálculo do índice LW os dados de entrada necessários são os percentuais de votação que cada partido recebeu em cada eleição, dentro de um determinado período de tempo.
Exemplo: A partir dos dados da Tabela 5 e do peso padrão 20, por eleição, temos. A primeira etapa é calcular os votos com a aplicação dos pesos para cada partido, assim, temos: PARTIDO A; percentual por eleição: eleição 1 – 51,2%; eleição 2 – 46,8% x 1,2 = 56,16%; eleição 3 – 30,4% x 1,4 = 42,56%; eleição 4 – 27,2% x 1,6 = 43,5,2%; eleição 5 – 36,2% x 1,8 = 65,16%; eleição 6 – 29,4% x 2 = 58,8%; eleição 7 – 15,9% x 2,2 = 34,98%; eleição 8 – 30,1% x 2,4 = 72,24%; eleição 9 – 35,6% x 2,6 = 92,56%; eleição 10 – 32,0% x 2,8 = 89,6%. PARTIDO B; percentual por eleição: eleição 1, – 44,3%; eleição 2 – 42,4% x 1,2 = 50,88%; eleição 3 – 42,1% x 1,4 = 58,94%; eleição 4 – 38,5% x 1,6 = 61,6%; eleição 5 – 31,7% x 1,8 = 57,06%; eleição 6 – 32,9% x 2 = 65,8%; eleição 7 – 36,7% x 2,2 = 80,74%; eleição 8 – 7,8% x 2,4 = 18,72%; eleição 9 – 21,5% x 2,6 = 55,9%; eleição 10 – 29,5% x 2,8 = 82,66%. PARTIDO C; percentual por eleição: eleição 1, – 4,5%; eleição 2 – 10,8% x 1,2 = 12,96%; eleição 3 – 27,5% x 1,4 = 38,5%; eleição 4 – 34,3% x 1,6 = 54,88%; eleição 5 – 29,2% x 1,8 = 52,56%; eleição 6 – 33,0% x 2 = 66,0%; eleição 7 – 42,4% x 2,2 = 93,28%; eleição 8 – 58,3% x 2,4 = 139,92%; eleição 9 – 37,8% x 2,6 = 98,28%; eleição 10 – 35,2% x 2,8 = 98,56%. PARTIDO D; percentual por eleição: eleição 5 – 2,9%; eleição 6 – 1,8% x 1,2 = 2,16%; eleição 7 – 1,7% x 1,4 = 2,38%; eleição 8 – 2,3% x 1,6 = 3,68%; eleição 9 – 2,3% x 1,8 = 4,14%; eleição 10 – 1,1% x 2 = 2,2%. PARTIDO E; percentual por eleição: eleição 6 – 2,9%; eleição 7 – 3,2% x 1,2 = 3,84%; eleição 8 – 1,5% x 1,4 = 2,1%; eleição 9 – 2,8% x 1,6 = 4,48%; eleição 10 – 2,2% x 1,8 = 3,96%. A segunda etapa é somar os percentuais finais para cada eleição considerando o histórico. Assim temos: Eleição 1 – 100%; Eleição 2 – 120% + 100% = 220%; Eleição 3 – 140% + 220% = 360%; Eleição 4 – 160% + 360% = 520%; Eleição 5 – 177,68% + 520% = 697,68%; Eleição 6 – 195,66 + 697,68% = 893,34%; Eleição 7 – 215,22% + 893,34% = 1108,56%; Eleição 8 – 236,66% + 1108,56% = 1345,22%; Eleição 9 – 255,36% + 1345,22% = 1600,58%; Eleição 10 – 276,98% + 1600,58% = 1877,56%. A terceira etapa é calcular os valores nocionais, para cada eleição, assim temos: Eleição 1 – 100%; Eleição 2 – 120% + 100% = 220%; Eleição 3 – 140% + 220% = 360%; Eleição 4 – 160% + 360% = 520%; Eleição 5 – 180% + 520% = 700%; Eleição 6 – 200% + 700% = 900%; Eleição 7 – 220% +900% = 1120%; Eleição 8 – 240% + 1120% = 1360%; Eleição 9 – 260% + 1360% = 1620%; Eleição 10 – 280% + 1620% = 1900%. Por fim, a última etapa é calcular os índices LW para cada eleição, dividindo os valores da etapa 2 pelos respectivos valores da etapa 3. Assim temos: Eleição 1 – LW = 100%; Eleição 2 – LW = 100%; Eleição 3 – LW = 100%; Eleição 4 – LW = 100%; Eleição 5 – LW = 99,66%; Eleição 6 – LW = 99,26%; Eleição 7 – LW = 98,97%; Eleição 8 – LW = 98,91%; Eleição 9 – LW = 98,80%; Eleição 10 – LW = 98,81%. Estes são os valores históricos do índice LW a partir da Tabela 5.
8.3: Índice de Dominância dos Partidos Estabelecidos
Conceitos: O índice de Dominância dos Partidos Estabelecidos (EDP) possui, conceitualmente, a mesma ideia do índice LW. Entretanto existe uma diferença quanto ao peso. No caso do índice LW o peso de 20% é atribuído conforme as eleições, sem considerar o tempo entre elas. Já no índice EDP o valor do peso é 5%, e é atribuído por ano. Assim, conforme a distância em anos entre cada eleição assim será o peso. Para um ano o peso é 5%; para dois anos é 10%, e assim por diante. A diferença entre o índice LW e o índice EDP é que o primeiro considera eleições sequenciais e o segundo a distância temporal entre eleições sequenciais.
A ideia do índice LW é verificar a estabilidade do sistema partidário entre eleições, independentemente do tempo que isso ocorra. Já o índice EDP verifica a estabilidade do sistema partidário entre eleições considerando o tempo em que elas ocorram. À exceção da atribuição dos pesos, todo o restante é igual em termos de cálculo e em termos conceituais.
Interpretação: O índice de Dominância dos Partidos Estabelecidos (EDP) é lido de forma direta. Quanto maior o valor, maior é o nível da manutenção do sistema partidário na linha do tempo. Se o valor aumenta de uma eleição para outra, isso significa que a manutenção do sistema partidário continua constante. Entretanto, se o valor diminui entre eleições, certamente, a dominância diminuiu, o que pode ocorrer pela menor quantidade de votos dedicados aos partidos pelos eleitores.
Dados de Entrada: Tal como o índice LW, para o índice EDP os dados de entrada são os percentuais de votação que cada partido recebeu em cada eleição, dentro de um determinado período de tempo.
Exemplo: A partir dos dados da Tabela 5 e do peso padrão 5, por ano, temos. A primeira etapa é calcular os votos com a aplicação dos pesos para cada partido, assim, temos: PARTIDO A; percentual por eleição: eleição 1, – 51,2%; eleição 2 – 46,8% x 1,2 = 56,16%; eleição 3 – 30,4% x 1,3 = 39,52%; eleição 4 – 27,2% x 1,45 = 39,44%; eleição 5 – 36,2% x 1,5 = 54,3%; eleição 6 – 29,4% x 1,7 = 49,98%; eleição 7 – 15,9% x 1,8 = 28,62%; eleição 8 – 30,1% x 1,9 = 57,19%; eleição 9 – 35,6% x 2,1 = 74,76%; eleição 10 – 32,0% x 2,3 = 73,6%. PARTIDO B; percentual por eleição: eleição 1, – 44,3%; eleição 2 – 42,4% x 1,2 = 50,88%; eleição 3 – 42,1% x 1,3 = 54,73%; eleição 4 – 38,5% x 1,45 = 55,825%; eleição 5 – 31,7% x 1,5 = 47,55%; eleição 6 – 32,9% x 1,7 = 55,93%; eleição 7 – 36,7% x 1,8 = 66,06%; eleição 8 – 7,8% x 1,9 = 14,82%; eleição 9 – 21,5% x 2,1 = 45,15%; eleição 10 – 29,5% x 2,3 = 67,85%. PARTIDO C; percentual por eleição: eleição 1, – 4,5%; eleição 2 – 10,8% x 1,2 = 12,96%; eleição 3 – 27,5% x 1,3 = 35,75%; eleição 4 – 34,3% x 1,45 = 49,735%; eleição 5 – 29,2% x 1,5 = 43,8%; eleição 6 – 33,0% x 1,7 = 56,1%; eleição 7 – 42,4% x 1,8 = 76,32%; eleição 8 – 58,3% x 1,9 = 110,77%; eleição 9 – 37,8% x 2,1 = 79,38%; eleição 10 – 35,2% x 2,3 = 80,96%. PARTIDO D; percentual por eleição: eleição 5 – 2,9%; eleição 6 – 1,8% x 1,2 = 2,16%; eleição 7 – 1,7% x 1,3 = 2,21%; eleição 8 – 2,3% x 1,4 = 3,22%; eleição 9 – 2,3% x 1,6 = 3,68%; eleição 10 – 1,1% x 1,8 = 1,98%. PARTIDO E; percentual por eleição: eleição 6 – 2,9%; eleição 7 – 3,2% x 1,1 = 3,52%; eleição 8 – 1,5% x 1,2 = 1,8%; eleição 9 – 2,8% x 1,4 = 3,92%; eleição 10 – 2,2% x 1,6 = 3,52%. A segunda etapa é somar os percentuais finais para cada eleição considerando o histórico. Assim temos: Eleição 1 – 100%; Eleição 2 – 120% + 100% = 220%; Eleição 3 – 130% + 220% = 350%; Eleição 4 – 145% + 350% = 495%; Eleição 5 – 148,55% + 495% = 643,55%; Eleição 6 – 167,07 + 643,55% = 810,62%; Eleição 7 – 176,73% + 810,62% = 987,35%; Eleição 8 – 187,8% + 987,35% = 1175,15%; Eleição 9 – 206,89% + 1175,15% = 1382,04%; Eleição 10 – 227,91% + 1382,04% = 1609,95%. A terceira etapa é calcular os valores nocionais, para cada eleição, assim temos: Eleição 1 – 100%; Eleição 2 – 120% + 100% = 220%; Eleição 3 – 130% + 220% = 350%; Eleição 4 – 145% + 350% = 495%; Eleição 5 – 150% + 495% = 645%; Eleição 6 – 170% + 645% = 815%; Eleição 7 – 180% + 815% = 995%; Eleição 8 – 190% + 995% = 1185%; Eleição 9 – 210% + 1185% = 1395%; Eleição 10 – 230% + 1395% = 1625%. Por fim, a última etapa é calcular os índices EDP para cada eleição, dividindo os valores da etapa 2 pelos respectivos valores da etapa 3. Assim temos: Eleição 1 – EDP = 100%; Eleição 2 – EDP = 100%; Eleição 3 – EDP = 100%; Eleição 4 – EDP = 100%; Eleição 5 – EDP = 99,77%; Eleição 6 – EDP = 99,46%; Eleição 7 – EDP = 98,23%; Eleição 8 – EDP = 99,16%; Eleição 9 – EDP = 99,07%; Eleição 10 – EDP = 99,07%. Estes são os valores históricos do índice EDP a partir da Tabela 5.
8.4: Idade Partidária
Conceitos: Idade Partidária ou ainda Tempo Médio de Vida Partidária (Tp), não se trata de um índice, mas um valor que a partir de algumas premissas permite indicar a idade média partidária para uma dada eleição. Para que um dado partido possa contabilizar seu valor no cálculo a seguinte premissa deve ser preenchida: Que o partido na dada eleição tenha recebido ao menos 3% dos votos. Os partidos que tiverem valor inferior não fazem parte do cálculo. O valor de 3% sugere uma linha de corte para o cálculo.
A idade partidária, entre outras coisas, dá ideia da mobilização partidária. Se a idade média é baixa, indica a existência de muitos partidos recém criados, o que permite inferir duas coisas. A primeira é que a insatisfação popular é alta e isso se reflete na criação de novos partidos. A segunda é que houve alteração recente no sistema político/eleitoral. Caso a idade média seja alta, indica a persistência dos partidos ao longo do tempo, ou seja, que existe certa ordem organizacional que garante a permanência dos partidos. Em outras palavras representa que o os partidos e os seus sistemas organizacionais, ambos há muito estabelecidos, além de persistirem não foram substituídos por novos partidos.
A média utilizada para o cálculo é a média aritmética. Se usada média ponderada para o cálculo da idade partidária, utilizando o percentual de votos de cada partido considerado como peso de ponderação, então teremos ideia se a sociedade apoia mais novas ideias ou se esta se mantém arraigada nas mesmas ideias. Neste caso, se a idade partidária é baixa, indica que a sociedade não está em conformidade com as velhas ideias e busca nas novas ideias uma solução. A idade média pode ainda ser calculada através de ponderação em função do tempo de existência, o que resultaria em outro resultado, indicando a idade média em função da persistência dos partidos.
Exemplo: A partir da Tabela 5, temos as seguintes idades cronológicas dos partidos, com referência ao ano de 2024, Partido A, 44; B, 42; C, 30; D, 20 e E, 19. Entretanto, o critério exige que o partido tenha alcançado 3% de votos em alguma eleição, e, nesse sentido, o Partido D não cumpre esse critério. Logo, a idade cronológica do Partido D não é contabilizada no cálculo. Logo, a partir da média aritmética das idades cronológicas dos partidos A, B, C e E, temos a idade partidária que vale 33,75 anos; ou ainda 33 anos e 9 meses.
8.5: Índice de Institucionalização Partidária
Conceitos: Esse índice mensura, ao mesmo tempo, o nível de organização interna dos partidos e a capacidade adquirida por eles, ao longo do tempo, de movimentar a sociedade e suas opiniões. A medida não é unitária, ou seja, não é uma medida por partido, mas o conjunto deles, de forma que a medida é global, logo, o índice é uma mensuração do Sistema Partidário, este formado por todos os partidos na arena política.
O cálculo utiliza dois parâmetros, já abordados. A idade média dos partidos (Tp) que é, na verdade a idade média do conjunto formado por todos os partidos que atuam nas eleições considerando uma linha de corte com base nas votações obtidas. Esse índice mede o nível de permanência e persistência de um partido. Além da sua organização institucional, permite inferir a mobilidade partidária e a formação de novos partidos em conjunto e, se conhecido o segundo, permite ainda ter uma visão mais clara da realidade institucional em uma análise conjunta.
O segundo índice é o EDP. Ele mensura o nível de preferência geral do eleitorado com relação aos partidos. Indica se há preferência histórica, por parte dos eleitores, ou se há alteração. Em outras palavras, indica o nível de aceitação dos partidos e suas configurações, ou seja, do status quo político. Assim, a idade média mensura a organização interna dos partidos de forma global e o EDP mensura o nível de aceitação dos partidos de uma forma global. Um índice está associado a questões internas dos partidos e outro está associado ao nível de aceitação por parte dos eleitores, ou seja, uma medida externa aos partidos. Desta forma é calculado o Índice de Institucionalização Partidária (Tp). Ele considera um fator interno aos partidos (idade média) e um fator externo a eles (EDP).
Equação: A equação 23 calcula o IP. < TERMINAR!!! >
ESCREVER A EQUAÇÃO 23 AQUI!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
8.6: Critério de Número de Novos Partidos
Conceitos: Não se trata de um índice, mas uma ideia que a partir de algumas premissas permite contabilizar novos partidos (NP). A ideia foi proposta por Sikk, no ano de 2005. Para contabilizar como um novo partido, as seguintes premissas devem ser preenchidas em sua totalidade, são elas:
1: É considerado um novo partido quando ele não é uma sucessão de outro partido, tendo surgido per se.
2: É considerado um novo partido quando ele possui um nome novo.
3: É considerado um novo partido quando ele possui uma estrutura própria, criada para esse fim, não tendo estrutura adquirida de outro partido.
4: É considerado um novo partido quando ele não é originado de fusões partidárias ou coligações eleitorais já existentes.
5: É considerado um novo partido quando, após cumprir todos os quatro critérios anteriores, tenha obtido pelo menos 0,5% de votos.
6: Não é considerado um novo partido os partidos independentes.
Assim, desta forma, são contabilizados os novos partidos a partir dos critérios citados. Como pode ser notado, os critérios priorizam a inovação partidária, ou seja, a mobilização e a inovação dentro do sistema partidário.
9: Análises do Comportamento Partidário
São análises feitas para verificar o grau de coesão dos partidos dentro de uma casa legislativa ou dentro de um partido.
9.1: Índice de Disciplina Partidária
Proposição: Este índice tem vários proponentes em virtude de ser apresentado de formas diferentes. Cada uma das formas equacionadas teve um pensador diferente.
Equação: No presente caso temos três equações distintas, com ideia geral semelhante, entretanto, aplicadas para situações diferentes, resultando; portanto, em valores diferentes para o índice. As equações são apresentadas de forma genérica, conforme equação 24.
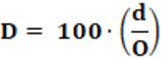
Conceitos: O Índice de Disciplina Partidária (D) pode ser apresentado com outras terminologias, tal como, Taxa de Fidelidade Partidária; entre outras denominações. O índice indica a ideia de unicidade da ação de um partido, em votações em uma casa legislativa, desde que haja uma orientação prévia por parte da liderança do partido a qual, em teoria, deve ser seguida pelos seus parlamentares.
O índice de disciplina partidária tem essa nomenclatura porque mensura, de forma percentual, a obediência dos parlamentares a seus partidos quanto a seguir as orientações nas votações, ou seja, votar conforme orientado pelas lideranças e o posicionamento oficial de seu partido na casa legislativa. Logo, por isso, o índice mede a disciplina dentro do partido, ou seja, a obediência institucional ao partido. Dito de outra forma, o índice D parte de uma regra institucional que o partido espera ser seguida pelos seus parlamentares. A votação; portanto, não é espontânea e mensura, na prática política, não a disciplina partidária, a partir dos parlamentares de um partido, mas sim a força que esse partido exerce sobre seus parlamentares. Em outras palavras, mensura a força de coerção de cada partido sobre seus parlamentares.
Pode também mensurar a fidelidade partidária, desde que os parlamentares assumam seu posicionamento e este esteja em conformidade com a orientação institucional do partido. Nesse caso mede a aceitação e concordância ideológica. Conceitualmente a fidelidade partidária e a disciplina partidária são distintas. Isso porque na disciplina partidária o voto orientado pelo partido é seguido pelo parlamentar mesmo que este não concorde, ao passo que, na fidelidade partidária, o parlamentar vota em conformidade à orientação partidária porque concorda, ideologicamente, com a ideia proposta. Vota por concordância e não por coerção. Entretanto, como é difícil obter dados quanto à intenção de votos e, o óbvio e comum é obter os dados a partir dos votos dados; pois, estes são visíveis, então é calculado o índice de disciplina partidária e, adota-se este como sendo o mesmo índice de fidelidade partidária, entretanto, como abordado, são índices, conceitualmente, diferentes. Em suma, a disciplina partidária mede a coerção do partido e a fidelidade partidária mede uma ação espontânea do parlamentar. O primeiro parte do partido em direção ao parlamentar e o segundo parte do parlamentar em direção ao partido.
Feito esse esclarecimento, segue a análise para cada da equação e suas alterações, conforme equação 25. O primeiro a abordar é que “d” representa a quantidade de vezes que o parlamentar seguiu a disciplina partidária, votando, na casa legislativa, em conformidade à orientação recebida pelo partido. Esse parâmetro é constante. O que altera é o parâmetro “O” que pode ter três valores distintos, a saber: “(OP)–“, usado quando o parlamentar esteve presente na casa legislativa e houve orientação por parte do partido para votar “sim” ou “não” (equação 25a); “(OT)–“, usado sempre que o partido orientou a votação na casa legislativa apenas como “sim” ou “não”, independentemente da presença do parlamentar na casa (equação 25b) e “(OT)+“, usado sempre que o partido orientou a votação na casa legislativa para qualquer direção, incluindo além do “sim” e “não”, também obstruções, independentemente da presença do parlamentar na casa (equação 25c).
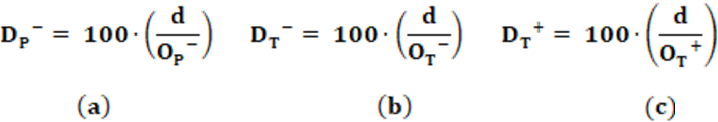
Diante das equações podemos facilmente afirmar que (OP)– < (OT)– porque (OT)– considera a presença ou não do parlamentar, o que faz com que (OP)– seja menor ou no máximo igual a (OT)– , o que ocorre quando o parlamentar não faltou quando o partido realizou a orientação na votação. De forma análoga (OT)– < (OT)+ porque (OT)+ considera todas as orientações, não somente votar “sim” ou “não”. Logo; temos: (DP)– > (DT)– > (DT)+ . O índice D deve ser calculado dentro de um dado período temporal e não apenas em uma única votação. Uma observação importante sobre o índice D é que valores baixos indicam indisciplina partidária o que pode indicar uma crise intrapartidária.
Uma observação interessante é adotar uma margem de corte para os casos onde a maioria, na casa legislativa, foi muito acentuada. Por exemplo, para casos onde 90% dos parlamentares votaram da mesma forma, nesse caso a disciplina partidária não é medida que possa conferir uma medida real, uma vez que não houve conflito, momento onde a disciplina partidária é medida importante a ser mensurada.
Interpretação: A interpretação do índice D é direta e vista através do valor percentual calculado. Valores altos indicam alta disciplina partidária e valores baixos indicam baixa disciplina partidária. É comum valores acima de 90%. Extremamente raros são valores abaixo deste percentual.
Dados de Entrada: Para determinar o índice D, é necessário ter acesso aos votos dos parlamentares e a indicação dos partidos, bem como o confronto destas informações para estimar o parâmetro “d”.
Exemplo: A partir dos dados da tabela 6, considerando que a coluna 1 corresponde a parlamentares de um mesmo partido, que +1 corresponde a voto no mesmo sentido da orientação das lideranças partidárias; que -1 corresponde a voto contrário ao orientado pelas lideranças partidárias e 0 é quando as lideranças partidárias não orientaram o voto, assim, temos: Parlamentar 1; 3/4 = 75%; Parlamentar 2; 4/4 = 100%; Parlamentar 3; 3/4 = 75%; Parlamentar 4; 1/4 = 25%; Parlamentar 5; 3/4 = 75%; Parlamentar 6; 1/4 = 25%; Parlamentar 7; 3/4 = 75%; Parlamentar 8; 2/4 = 50%. Essa é a disciplina partidária para cada parlamentar. Este é um resultado. Realizada a média aritmética dos valores da disciplina partidária de cada parlamentar temos a disciplina partidária, supondo que este tenha 8 parlamentares. Assim, temos que a disciplina partidária é 62.5%.
9.2: Índice Rice de Coesão Intrapartidária
Proposição: O nome do índice Rice (R) é uma homenagem ao estatístico e sociólogo estadunidense Stuart Arthur Rice, idealizador do mesmo.
Equação: A equação que calcula o índice R é apresentada na equação 26.
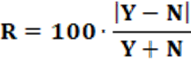
A mesma equação, após alguns manejos algébricos, pode ser reescrita conforme apresentada na equação 27.
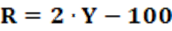
Conceitos: O índice Rice (R) é também conhecido como Índice de Coesão Partidária; Taxa de Coesão Intrapartidária; Taxa de Unidade Partidária e qualquer outro que confira a ideia de concordância nas votações na casa legislativa por parte dos parlamentares de um partido qualquer. Este índice não parte do princípio de que há uma orientação prévia da liderança do partido aos seus parlamentares. Logo, difere, conceitualmente, e, matematicamente, do índice de disciplina partidária (D). Pode ainda ser expandido para a coesão dentro da casa legislativa, passando a ser um índice interpartidário.
Isso porque a votação do parlamentar é espontânea, sem a coerção a partir da orientação partidária. Mesmo que exista orientação partidária e o parlamentar vota conforme sua própria vontade, o fato de existir uma orientação afeta o valor do índice R porque outros parlamentares poderão alterar sua intenção de voto em função da orientação do partido.
Portanto; só é tomado como válido o índice R quando não existe orientação partidária para votação na casa legislativa. A ideia é indicar o valor de coesão partidária entre os parlamentares, que é uma medida espontânea, livre da coerção do próprio partido. A coesão permite, por inferência, estimar o nível de fidelidade partidária (não confundir com disciplina partidária). O grande valor do índice R é permitir verificar, em situações livres de pressão institucional, como está a unidade de pensamento e decisão dos parlamentares de um mesmo partido. Permite, inferir, pelo valor do índice R, uma crise intrapartidária e ideológica.
Interpretação: A interpretação do índice R, tal como o índice anterior, é direta e vista através do próprio valor percentual calculado. Valores altos indicam alta coesão partidária e valores baixos indicam baixa coesão partidária.
Dados de Entrada: Para determinar o índice R, é necessário ter somente a quantidade percentual de votos “sim”. Com estas informação estima-se o parâmetro “R”.
Exemplo: A partir dos dados da tabela 6, considerando que a coluna 1 corresponde a parlamentares de um mesmo partido, que +1 corresponde a voto “SIM” a determinado projeto de Lei, que -1 corresponde a voto “NÃO” ao mesmo projeto de Lei e desconsiderando as colunas com indicação “0”; assim, temos. Projeto de Lei 1: Y = 6, N = 2; Projeto de Lei 3: Y = 7; N = 1; Projeto de Lei 4: Y = 5, N = 3; Projeto de Lei 5: Y = 5, N = 3. A próxima etapa é estimar o percentual de “Y” para cada Projeto de Lei, assim, temos; Y1 = 100 x (6/8) = 75%; Y3 = 100 x (7/8) = 87,5%; Y4 = 100 x (5/8) = 62,5%; Y5 = 100 x (5/8) = 62,5%. Se for feita a média aritmética destas quatro votações teremos o índice R destas quatro votações, o que resulta 71,87%. A análise pode ser feita para um partido (intrapartidário) ou para toda a casa legislativa (parlamento).
10: Análises do Governo (Executivo)
São análises feitas para analisar o governo, quanto a sua capacidade de governar e nível de aceitação parlamentar, bem como a força de um governo e sua aceitação popular.
10.1: Índice Percentual de Polarização
Proposição: A Polarização pode ser medida de forma simples e com certo grau de confiança, ainda que aspectos políticos não lineares ou imprevistos podem afetar a confiança desta medida. O índice percentual de Polarização (POL) foi proposto em 1976 por Sartori (Giovanni Sartori; Cientista Político – Itália).
Equação: A equação que calcula o índice POL é apresentado na equação 28.
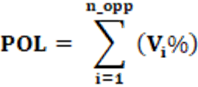
Conceitos: Conceitualmente, a polarização é medida segundo o percentual que se oponha ao governo em exercício. Caso a equação utilize o total de cadeiras da casa legislativa conquistadas pelos partidos de oposição, a polarização é de tipo legislativa. Caso a equação utilize os votos dos eleitores concedidos a esses partidos, isso representa a polarização existente na sociedade. Este é o caso da equação 28. A polarização é indicada por n_opp; onde “n” considera todos os partidos em uma eleição, já “n_opp” considera somente os partidos de oposição.
Para que um partido seja categorizado como partido de oposição ele deve ter que preencher, simultaneamente, três critérios. São eles: 1: É um partido que se coloca em oposição aos partidos que compõem os partidos que apoiam o governo. 2: O partido tem um discurso onde afirma haver uma distância entre a política e a sociedade. 3: Afirma e trabalha para alterar o status quo, de forma trazer grandes alterações políticas e no sistema político. Assim, todo partido que preencha todos esses três critérios é considerado partido de oposição. Todo partido de oposição entra na somatória da equação 28.
Interpretação: A interpretação do índice POL é simples e direta. O valor resultante do índice POL é o valor percentual da polarização. Recorda-se que a equação 28 utiliza o percentual de votos, o que represente a polarização da sociedade ao governo e partidos que o apoiam. Caso seja usado a quantidade percentual de cadeiras na casa legislativa, essa polarização é legislativa, conforme já dito.
Dados de entrada: Para calcular o índice POL é necessário somente um dado, e é a quantidade de votos obtidos por cada partido, em termos percentuais (Vi%). Após isso, há que aplicar os três critérios de oposição. Estes preenchidos, aplica-se a equação 28. Assim é calculado o índice POL.
Exemplo: A partir dos dados da tabela 6, considerando que a coluna 1 corresponde a partidos, que o sinal (+) corresponde a partido a favor do governo e (-) corresponde a partido de oposição, a polarização se dá a partir da soma que cada partido de oposição recebeu nas eleições, o que está discriminado na última coluna. Assim, a polarização considera os partidos A, C, F e H; cujo valor de polarização resulta 55,3%.
10.2: Taxa de Coalescência
Conceitos: A taxa de coalescência (M) ou ainda conhecida como Taxa de Gabinete Ministerial mensura a diferença da proporção entre o número de cadeiras dos partidos no parlamento e a proporção dos partidos nos ministérios. Em outras palavras, mede o nível da proporção dos partidos no parlamento e nos ministérios. Para os propósitos do poder executivo, o ideal é que o índice seja zero, momento e que pi = mi. Não existe uma equação própria para calcular a Taxa de Coalescência. Para isso pode ser usada qualquer equação que calcule índices para verificar a proporcionalidade ou desproporcionalidade da representação dos partidos no sistema eleitoral. Isso inclui as equações dos índices de desvio linear, desvio quadrático e valores sobrerrepresentados.
Para isso há que ter claro que, conceitualmente, a taxa de coalescência calcula a diferença absoluta entre a proporção dos ministérios que um partido tem com a proporção de cadeiras que esse mesmo partido tem no parlamento. Assim, para o cálculo devemos utilizar índices que calculam a proporcionalidade. Nesse sentido o único índice direto de uso é o índice Rose (RO) que calcula a proporcionalidade da representação dos partidos no sistema eleitoral. Para os demais índices o uso não é direto porque eles calculam a desproporcionalidade e, para usá-los, temos que fazer uma pequena transformação que é subtrair o resultado de 1.
Ademais, fora isso, para qualquer dos casos o valor vi é substituído por mi, já pi é mantido. Devemos entender que mi é a proporção de ministérios que o partido i tem.
Equação: Para fins de ilustração é apresentada a equação 29 com suas alterações, para o índice Rose que para este caso é indicado como ROm. Também é apresentado o índice Gallagher adaptado para o caso, o que deve ser feito para todos os demais índices de desproporcionalidade. A indicação do índice Gallagher para este caso é LSqm.
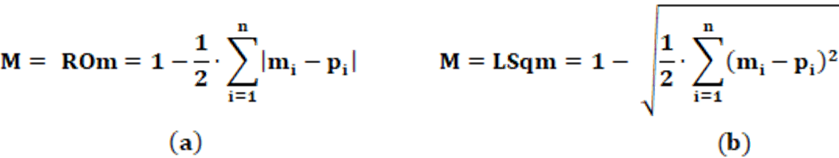
Interpretação: A interpretação do valor obtido é direta quando usado o índice Rose e deve ser espelhada quando é usado outro índice. Obviamente que o índice M varia em valor conforme a equação utilizada. Isso é o mesmo que ocorre com o cálculo dos índices para a representação dos partidos no sistema eleitoral. As ideias com vantagens e desvantagens dos índices são igualmente aplicadas aqui.
Exemplo: A partir dos dados das tabelas 6 e 7; com uso da equação M = ROm; e considerando o ano 2020; podemos calcular a taxa de coalescência. O primeiro é ter claro que os valores percentuais da tabela 6 devem ser transformados em índices, ou seja, dividir por 100. A segunda etapa é calcular a proporção de cadeira para cada partido, como segue: Partido A, pi = 10/25 = 0,4; Partido B, pi = 6/25 = 0,24; Partido C, pi = 4/25 = 0,16; Partido D, pi = 3/25 = 0,12; Partido E, pi = 2/25 = 0,08. A terceira etapa é calcular a diferença absoluta para cada partido; Partido A, |vi-pi| = 0,08; Partido B, |vi-pi| = 0,055; Partido C, |vi-pi| = 0,192; Partido D, |vi-pi| = 0,109; Partido E, |vi-pi| = 0,058. A quarta etapa é calcular a taxa de coalescência, que resulta 0,753 (75,3%).
10.3: Avaliação de Apoio Presidencial
Conceitos: A Avaliação de Apoio Presidencial (GOV) é uma medida percentual que indica o nível de apoio que o poder executivo tem junto ao poder legislativo. É uma medida de força e prestígio do executivo e de seu governo. Permite identificar a capacidade de governar do presidente. O apoio ao executivo tem relação com as votações no parlamento, geralmente, a Câmara dos Deputados Federais; pois, é usada como referência para fins de política comparada. A ideia é simples e devemos considerar que o índice deve ser mensurado a partir de um determinado período de tempo. Interessante uma análise mensal e ter estas informações apresentadas em gráfico para fácil interpretação visual dos dados, ao longo de um ano. O índice é calculado a partir da relação entre os votos a favor do governo com relação aos votos totais. O valor é apresentado na forma percentual.
Equação: A equação possui a mesma ideia da equação para mensurar a disciplina partidária. Ela é mostrada na equação 30.
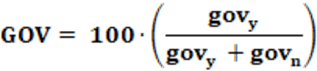
Interpretação: A interpretação do valor é direta. Valores altos da taxa GOV indicam maior apoio do legislativo ao executivo e melhor governabilidade, com menor custo político e menos propenso a crises. Valores baixos da taxa GOV indicam menor apoio do legislativo ao executivo e governabilidade mais difícil, com maior custo político e com maior probabilidade de crises.
Dados de entrada: Para estimar a taxa GOV é necessário ter os votos na cada legislativa a favor e contra o governo, Há que saber a orientação do governo em cada votação. Os valores devem compreender determinado período de tempo, do contrário, a taxa não reproduz a realidade. Dar preferência por votações onde exista oposição, do contrário, a taxa GOV não reproduzirá a realidade.
Exemplo: A partir dos dados da tabela 6, considerando que a coluna 1 corresponde a parlamentares de partidos diversos, que +1 corresponde voto a favor da expectativa do governo a determinado projeto de Lei, que -1 corresponde voto contra a expectativa do governo a determinado projeto de Lei, e considerando que as colunas com indicação “0” representam indiferença do governo; assim, temos. Projeto de Lei 1: govy = 6, govn = 2; Projeto de Lei 3: govy = 7; govn = 1; Projeto de Lei 4: govy = 5, govn = 3; Projeto de Lei 5: govy = 5, govn = 3. Assim, temos; Projeto de Lei 1, GOV = 75%; Projeto de Lei 3, GOV = 87,5%; Projeto de Lei 4, GOV = 62,5%; Projeto de Lei 5, GOV = 62,5%. Neste caso, como os dados da tabela são os mesmos, os valores do índice GOV resultaram os mesmos valores da taxa de coesão intrapartidária, entretanto, com dados reais, isso dificilmente acontece. Por fim, podemos fazer a média aritmética para estimar o índice GOV, que resulta 71,87%.
10.4: Avaliação de Desempenho Político-Institucional
O primeiro a informar é que não existe um índice único ou uma taxa única que mensure a Avaliação de Desempenho Político-Institucional, representado, de forma genérica pela letra grega ε. Há várias formas de realizar essa mensuração. Há medidas feitas por todos os países devido a terem um caráter técnico, lógico e prático, é o caso da inflação, índice de desemprego, índice de crescimento anual, produto interno, entre outros. São análises que partem da economia e áreas correlatas.
Há ainda medidas criadas para comparar resultados entre países, é o caso, por exemplo, do índice de Gini e do índice PISA. Há outros índices que fazem medidas comparativas entre países. Existe, por exemplo, o índice de felicidade.
No nosso caso importa somente apontar que uma análise ε deve considerar várias áreas de atuação do governo, porque a avaliação é do desempenho do poder executivo. Por lógico, não há um índice único. Para uma análise mais efetiva é interessante separar as análises em três categorias: indicadores gerenciais; indicadores estratégicos e indicadores operacionais. Desta forma temos uma visão mais bem elaborada e de análise mais afinada com a realidade. Estes indicadores são categorizados como indicadores hierárquicos.
Qualquer indicador deve preencher três requisitos básicos: i – ter coleta de dados metódica; ii – deve ainda ter dados coletados de forma periódica e iii – deve representar a realidade daquilo que mensura. Além disso a análise deve ter caráter cumulativo, com o intuito de gerar dados na linha do tempo, para melhor interpretação. Independentemente do índice e o que mensurar, os índices devem preencher esse requisitos.
Um dos profissionais que deve trabalhar na elaboração de índices para análise governamental são os cientistas políticos. Entretanto, é comum indicadores construídos por economistas, matemáticos, estatísticos e engenheiros.
10.5: Índice de Fechamento do Sistema Partidário
Conceitos: O índice de Fechamento Partidário (X) indica o quão aberto um sistema partidário está para mudanças. Ele é mensurado através das mudanças ministeriais e os partidos que assumem estas pastas. O índice X é um índice temporal, que considera o histórico de mudanças. Existem três elementos que permitem o cálculo do índice X, são eles: alternância; fórmula e acesso.
Alternância (ALT) faz referência à diferença das pastas ministeriais obtidas por cada partido entre composições ministeriais consecutivas (eleições consecutivas). Ou seja, devemos considerar a eleição e e a eleição e-1 e suas composições ministeriais. O cálculo é semelhante ao índice Pedersem, entretanto, a diferença reside que usamos as pastas ministeriais de cada partido. Como dito, a diferença considera duas eleições consecutivas (composições ministeriais) e utiliza todos os partidos no cálculo, os que se mantém com pastas na eleição e e aqueles que só tiveram pastas na eleição e-1. O valor calculado é o valor da alternância. Este valor deve estar sempre entre 50 e 100, caso seja menor que 50, devemos subtrair esse valor de 100, e este será o resultado da alternância, caso contrário o valor calculado é o próprio valor da alternância.
No caso a Fórmula (FOR) tem relação com a inovação no governo, é a fórmula que o governo usa para composição dos ministérios. A fórmula tem três tipos de valores. Se há inovação total, o que ocorre quando não há repetição de partidos compondo um mesmo grupo partidário nos ministérios, o valor da fórmula é 0. Isso ocorre quando a composição é única dentro do período analisado. Caso não haja inovação alguma, o que ocorre quando na eleição analisada os partidos se repetem em algum momento do passado, o valor será 100, desde que na eleição analisada estes partidos se repitam em sua totalidade ou somente parte dele. Caso a repetição dos partidos seja total ou parcial, mas exista a presença de um partido novo que cria nova composição nos ministérios; algo que ainda não ocorreu, o valor da fórmula é a soma dos valores percentuais dos partidos recorrentes. Neste último caso a fórmula não é inovadora ou sem inovação, mas sim de inovação parcial. Por isso o valor ficará sempre maior que 0 e menor que 100.
Por fim, o Acesso (ACC) tem ideia semelhante à Fórmula, entretanto, no lugar de considerar grupos partidários, considera o acesso de partidos aos ministérios. O acesso terá valor 0 se há acesso de partidos que nunca assumiram pastas ministeriais. O acesso terá valor 100 se todos os partidos já tiveram acesso a pastas ministeriais. Caso parte dos partidos tenha tido acesso e outra parte não tenha tido acesso, o valor do acesso será a soma dos percentuais dos partidos que já tenham tido acesso aos ministérios, ou seja, desconsidera os partidos que tenham acesso pela primeira vez. De forma semelhante à fórmula, o acesso utiliza reconhecer as recorrências e não as novidades.
Ao fim destes valores calculamos a média de cada um destes três valores. Da média da alternância aplicamos uma correção, já que a escala está entre 50 e 100 e devemos corrigir para uma escala de 0 a 100. Para isso aplicamos a equação 31. Feito isso, aplicamos a equação 32 e obtermos o valor do índice de fechamento do sistema partidário (X).
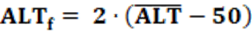
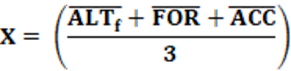
O índice de Fechamento do Sistema Partidário (X) permite mensurar a Institucionalização do Sistema Partidário (PSI). Este índice é de grande valia para análises mais profundas dos partidos e dos sistemas partidários. Várias são as possibilidades para mensurar PSI, e uma delas é o índice X que traz bons resultados porque tem implícito nos cálculos a fragmentação partidária, a volatilidade eleitoral, a estabilidade do sistema partidário e eleitoral, entre outros. Por isso o índice X é um dos modelos mais utilizados para mensurar a institucionalização do sistema partidário (PSI). O valor de PSI é o valor de X calculado.
Interpretação: A leitura do valor é direta. Quanto mais próximo de 100% maior é o fechamento do sistema partidário, ou seja, o sistema não se permite a inovações tanto na composição dos partidos, como nas suas composições em grupo. Também considera pouca variação da porporção dos ministérios. Para valores baixos, isso indica uma grande abertura quanto a mudanças. É comum valores acima de 80%.
Dados de entrada: Para o cálculo do índice X precisamos da quantidade de gabinetes ministeriais que cada partido tem ao longo do histórico a ser analisado. Esse valor deve estar na forma percentual.
Exemplo: Para fins de análise, para facilitar o estudo, apresentamos os dados na tabela 8. Junto a ela estão os resultados de alternância; fórmula e acesso. Na sequência temos as explicações pertinentes.
| i | Ano (Eleição) | Ministérios e Partidos (%) | ALT | FOR | ACC |
| 1 | 1986 (1) | A = 50; B = 20; C = 10; D = 10 | FG | FG | FG |
| 2 | 1987 | — | 100 | 100 | 100 |
| 3 | 1988 | — | 100 | 100 | 100 |
| 4 | 1989 | — | 100 | 100 | 100 |
| 5 | 1990 (2) | A = 55; B = 25; C = 20 | 85 | 100 | 100 |
| 6 | 1991 | — | 100 | 100 | 100 |
| 7 | 1992 | — | 100 | 100 | 100 |
| 8 | 1993 | — | 100 | 100 | 100 |
| 9 | 1994 (3) | E = 100 | 100 | 0 | 0 |
| 10 | 1995 | — | 100 | 100 | 100 |
| 11 | 1996 | — | 100 | 100 | 100 |
| 12 | 1997 | — | 100 | 100 | 100 |
| 13 | 1998 (4) | B = 25; E = 55; F = 20 | 55 | 0 | 80 |
| 14 | 1999 | — | 100 | 100 | 100 |
| 15 | 2000 | — | 100 | 100 | 100 |
| 16 | 2001 | — | 100 | 100 | 100 |
| 17 | 2002 (5) | A = 45; B = 15; G = 40 | 85 | 60 | 60 |
| 18 | 2003 | — | 100 | 100 | 100 |
| 19 | 2004 | — | 100 | 100 | 100 |
| 20 | 2005 | — | 100 | 100 | 100 |
| 21 | 2006 (6) | A = 30; H = 30; I = 40 | 70 | 0 | 30 |
| 22 | 2007 | — | 100 | 100 | 100 |
| 23 | 2008 | — | 100 | 100 | 100 |
| 24 | 2009 | — | 100 | 100 | 100 |
| 25 | 2010 (7) | A = 30; H = 50; J = 20 | 60 | 80 | 80 |
| 26 | 2011 | — | 100 | 100 | 100 |
| 27 | 2012 | — | 100 | 100 | 100 |
| 28 | 2013 | — | 100 | 100 | 100 |
| 29 | 2014 (8) | A = 20; B = 45; K = 35 | 80 | 65 | 65 |
| 30 | 2015 | — | 100 | 100 | 100 |
| 31 | 2016 | — | 100 | 100 | 100 |
| 32 | 2017 | — | 100 | 100 | 100 |
| 33 | 2018 (9) | A = 25; E = 15; F = 60 | 80 | 0 | 100 |
| 34 | 2019 | — | 100 | 100 | 100 |
| 35 | 2020 | — | 100 | 100 | 100 |
| 36 | 2021 | — | 100 | 100 | 100 |
| 37 | 2022 (10) | C = 15; D = 25; E = 20; F = 40 | 55 | 100 | 100 |
| 38 | 2023 | — | 100 | 100 | 100 |
| 39 | 2024 | — | 100 | 100 | 100 |
| TOTAL | — | 3.570 | 3.305 | 3.515 |
Explicação dos valores do exemplo: O primeiro é indicar um ano de referência que chamamos de Governo Financiador, assinalado como FG. A ele corresponde o início da análise. O segundo ponto é verificar os períodos entre eleições. Nesses períodos não há mudanças, assim assinalamos como 100 para todos os três elementos nos períodos entre eleições. Para os demais temos que fazer as análises pertinentes.
ALTERNÂNCIA: Corresponde à apliação da equação de Pedersen ajustada à presente situação, assim temos: (1990): ALT = (1/2) x |(55-50)+(25-20)+(20-10)+(0-10)| = 15. Como 15<50; então, 100-15 = 85. (1994): ALT = (1/2) x |(100-0)+(0-55)+(0-25)+(0-20)| = 100. (1998): ALT = (1/2) x |(55-100)+(25-0)+(20-0)| = 45. Como 45<50; então, 100-45 = 55. (2002): ALT = (1/2) x |(45-0)+(15-25)+(0-55)+(0-20)+(40-0)| = 85. (2006): ALT = (1/2) x |(30-45)+(0-15)+(0-40)+(30-0)+(40-0)| = 70. (2010): ALT = (1/2) x |(30-30)+(50-30)+(0-40)+(20-0)+(40-0)| = 40. Como 40<50; então, 100-40 = 60. (2014): ALT = (1/2) x |(20-30)+(45-0)+(0-50)+(0-20)+(35-0)| = 80. (2018): ALT = (1/2) x |(25-20)+(0-45)+(15-0)+(60-0)+(0-35)| = 80. (2022): ALT = (1/2) x |(0-25)+(15-0)+(25-0)+(20-15)+(40-60)| = 45. Como 45<50; então, 100-45 = 55.
FÓRMULA: Corresponde aos grupos partidários. (1990): Como os partidos A, B, C aparecem em 1986; então não houve inovação na composição, logo, 100. (1994): Como o partido E nunca apareceu, sendo uma configuração única, então houve inovação na composição, logo, 0. (1998): Como a configuração B, E, F é única, então houve inovação na composição, logo, 0. (2002): A configuração A, B, G até então não existiu, entretanto, a configuração A, B; sim; havendo inovação parcial; logo, a fórmula é a soma dos percentuais de A e B, logo 60. (2006): Como a configuração B, E, F é única, então houve inovação na composição, logo, 0. (2010): A configuração A, H, J até então não existiu, entretanto, a configuração A, H; sim; havendo inovação parcial; logo, a fórmula é a soma dos percentuais de A e H, logo 80. (2014): A configuração A, B, K até então não existiu, entretanto, a configuração A, B; sim; havendo inovação parcial; logo, a fórmula é a soma dos percentuais de A e B, logo 65. (2018): Como a configuração A, E, F é única, então houve inovação na composição, logo, 0. (2022): Aqui temos duas configurações recorrentes, C, D e E, F. Assim, da soma dos percentuais temos 100.
ACESSO: Corresponde aos partidos e o acesso aos ministérios. (1990): Os mesmos partidos em 1990 são os mesmos de 1986, assim os mesmos partidos tiveram acesso aos ministérios; logo, 100. (1994): O partido E teve seu primeiro acesso aos ministérios. (1998): O único partido novo é o F, assim o acesso é dado pela soma dos percentuais dos demais partidos, logo, 80. (2002): O único partido novo é o G, assim o acesso é dado pela soma dos percentuais dos demais partidos, logo, 60. (2006): Há dois partidos novos, H, I, assim o acesso é dado pelo percentual de A, logo, 30. (2010): O único partido novo é o J, assim o acesso é dado pela soma dos percentuais dos demais partidos, logo, 80. (2014): O único partido novo é o K, assim o acesso é dado pela soma dos percentuais dos demais partidos, logo, 65. (2018): Não há partido novo nos ministérios; logo, 100. (2022): Não há partido novo nos ministérios; logo, 100.
Com estes valores, calculamos a média dos três valores, que resultam em ALT = 91,53; FOR = 84,74; ACC = 90,12. O valor de ALTf a partir da equação 31, é 83,06. Por fim, aplicamos a equação 32 para obter X, que resulta 85,97%.
10.6: Índice da Potência Militar de um País
Proposição: O Índice da Potência Militar de um País (MW) foi criado em 2011, proposto por Sulek (Mirosław Sułek; Economista – Polônia). O índice mede a força miliar de um país a partir de valores relativos e, por consequência de sua própria conceituação, por meio de valores comparativos entre países, o que sugere uma ideia clara do poder bélico, mensurando a força militar.
Equação: A equação 33 apresenta o cálculo (apresentação adaptada).
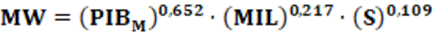
Conceitos: O índice faz uma avaliação da força militar de um dado país a partir de valores relativos entre os valores de todos os países do globo, em base 1000. Assim, o índice é um índice relativo o que sugere uma comparação direta, uma vantagem do índice. O parâmetro PIBM é o gasto militar do país analisado, em termos de PIB. É um valor relativo, já que considera, para um mesmo ano, a relação entre o gasto militar, em termos de PIB nacional do país analisado com relação ao gasto mundial, em termos de PIB mundial, de todos os países que vale, conceitualmente, 1000.
Devemos aplicar a mesma ideia aos outros dois parâmetros. O parâmetro MIL é a relação entre a quantidade de militares na ativa do país analisado com relação à quantidade de militares na ativa em todo o mundo, cujo valor atribuído é 1000. No mesmo raciocínio, S é a área relativa do país analisado com relação à área habitável do planeta (soma da área dos cinco continentes habitáveis), cujo valor atribuído é 1000.
Desta forma, a partir dos valores do país e do valor global, por meio de simples proporção, é possível obter os valores relativos em base 1000. Estes são os valores que devem ser usados na equação 33. Como a ideia é obter um índice que mede a potência militar, os gastos militares e a quantidade de militares na ativa permitem uma relação direta na leitura do índice. A área territorial é a área de atuação militar do país analisado. É onde o país exerce seu poder militar. Quanto maior a área do país maior é a área de ação militar.
Interpretação: A interpretação é de leitura direta. Quanto maior o índice maior é a potência militar. Devemos recordar que o índice é construído a partir de valores relativos. Logo, o índice infere uma medida relativa da potência militar.
Dados de entrada: Para o cálculo é necessário ter o valor de gasto militar do país a ser analisado em termos de PIB, bem como o valor total gasto no mundo. Devemos ter também posse da área do país analisado e a área dos cinco continentes habitáveis, dados de simples obtenção e de valores fixos, salvo mudanças geográficas. Por fim, temos que ter o número de militares na ativa, tanto no país a ser analisado como do mundo todo. Estes valores, ainda que se alterem de ano para ano, não têm alterações significativas.
Exemplo: Para este exemplo não temos tabela, usaremos os valores indicados diretamente aqui. Neste caso, para um ano qualquer, considerar um país com área territorial de 5.000.000 Km2; um gasto militar no valor de U$ 450.000.000 e com um contingente de 300.000 militares na ativa. Em termos mundiais, o gasto militar neste mesmo ano foi U$ 1.500.000.000.000; a quantidade de militares na ativa é de, aproximadamente, 20.500.000 e sendo a área dos 5 continentes algo em torno de 135.000.000 Km2; o valor do índice W é dado como segue. O primeiro a estimar é o PIBM cujo cálculo é (U$ 450.000.000/ U$ 1.500.000.000.000) x 1000 = 0,3. O segundo a estimar é o MIL cujo cálculo é (300.000 militares / 20.500.000 militares) x 1000 = 14,63. Por fim, estima-se S, calculado assim, (5.000.000 Km2/ 135.000.000 Km2) x 1000 = 37,03. Com estes valores calculamos W, que resulta 1,21.
11: Algumas Relações entre os Índices
Os índices podem ser calculados a partir de outros já que eles guardam relação entre si. Seguem as relações possíveis.
Relações entre RAE e ENP.
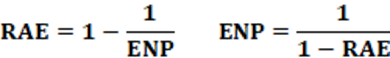
Relações entre RAED; LH; RO e G.
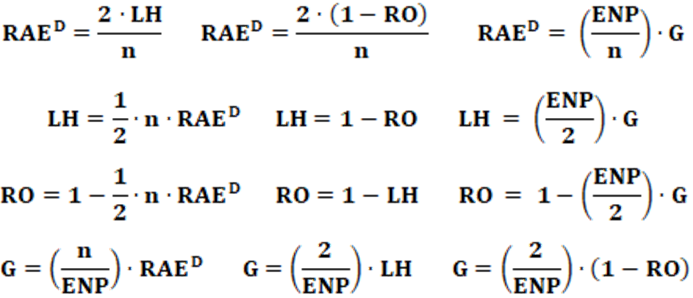
Relações entre LSq e MO.
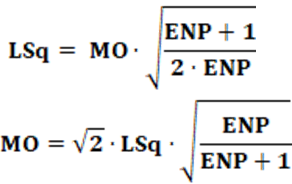
12: Resultados Práticos
Para fins de apresentar resultados reais, seguem os valores para o Brasil.
| RAE: 0,89 (ano, 2022) – 89% | MD: (ano, 2022) | PI: ** |
| ENP: 9,2 (ano, 2022) | LJ: (ano, 2022) * | NP: Partido Novo, em 2015 (ano, 2024) |
| RAED: 0,1009 (ano, 1998) – 10,09% | DH: (ano, 2022) * | D: 83% (PDT, mais indisciplinado; ano 2019) |
| LH: 0,0913 (ano, 1998) – 9,13% | W: 74,78% (ano, 2022 – eleições presidenciais, 1º turno) | R: 84,1% (anos, 2011-2014) |
| RO: 0,9087 (ano, 1998) – 90,87% | GAP: 1,8% (ano, 2022 – eleições presidenciais, 2º turno) | POL: 49,10% (ano, 2022 – eleições presidenciais) |
| G: 0,02571 (ano, 1998) – 2,57% | P: (ano, 2022) ** | M: 39% (ano, 2018) |
| LSq: 3,53 (ano, 2022) | LW: (período, 1998/2022; ano 2022) ** | GOV: 47% (ano, 2024 até mês de junho) |
| SL: * | EDP: (período, 1998/2022; ano 2022) ** | X: ** |
| MO: 4,74 (ano, 2022) | Tp: 24 anos e 5 meses (ano, 2024, mês 07) | MW: 7,2 |
13: Conclusões
Os índices e análises apresentadas permitem, por meio de valores, identificar aspectos da política institucional e, por eles, realizar análise comparativa entre países. A ideia não se esgota com a apresentação destes índices. Muitos outros existem e outros tantos são criados por pesquisadores que buscam facilitar a interpretação da realidade política por meio de uma análise quantitativa, o que confere uma interpretação mais intuitiva.
Não devemos comparar índices entre si e seus valores finais. Isso tem dois motivos, o primeiro é que cada qual tem sua construção particular, com sensibilidades a variações diferentes tanto na natureza do estímulo como na resposta que variações proporcionam no resultado. Segundo porque são escalas diferentes e a comparação direta é cometer erro conceitual. Logo, a comparação dos índices é para análise individual e comparação entre países, mas não entre índices, a não ser para realizar análises técnicas.
O uso de índices deve ser feito para análises mais profundas e devem ser difundidos e incentivados para serem usados no meio acadêmico e profissional. O incentivo de uso no meio acadêmico é caminho certo para uso no meio profissional. Assim a política encontra uma fonte de resposta a suas próprias variações e respostas no meio social de uma forma mais intuitiva.
REFERÊNCIAS BIBLIOGRÁFICAS
AIKATERINI, Kalogirou. Analysis and Comparison of the Greek Parliamentary Electoral Systems of the Period 1974-1999, chapter 5.
ARREDONDO, Verónica; MARTÍNEZ-PANERO, Miguel; PALOMARES, Antonio; PEÑA, Teresa; RAMÍREZ, Victoriano. NEW INDEXES FOR MEASURING ELECTORAL DISPROPORTIONALITY. Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA. Volumen 21(2020). Páginas 161 a 178; 2020.
BÉRTORA, Fernando Casal. POLITICAL PARTIES OR PARTY SYSTEMS? ASSESSING THE “MYTH” OF INSTITUTIONALIZATION AND DEMOCRACY.
BÉRTOA, Fernando Casal; ENYEDI, Zsolt; MÖLDER, Martin. PARTY AND PARTY SYSTEM INSTITUTIONALIZATION: WHICH COME FIRST? Cambridge University Press on behalf of the American Political Science Association; 2023.
COLLIRI, Tiago. EVALUATING PRESIDENTIAL SUPPORT IN THE BRAZILIAN HOUSE OF REPRESENTATIVES THROUGH A NETWORK-BASED APPROACH. University of Sao Paulo, Brazil
DEWAN, Torun; SPIRLING, Arthur. STRATEGIC OPPOSITION AND GOVERNMENT COHESION IN WESTMINSTER DEMOCRACIES. 2010.
DUTTA, Bhaskar. THE FRAGMENTED LOK SABHA: A CASE FOR ELECTORAL ENGINEERING. University of Warwick; 2009.
ENAP. ELABORAÇÃO DE INDICADORES DE DESEMPENHO INSTITUCIONAL. Brasília, 2013.
FARID, Wadjdi, A.; MISTIANI; NEBULA F., Hasani. THE MULTI-PARTY SYSTEM IN INDONESIA: REVIEWING THE NUMBER OF ELECTORAL PARTIES FROM THE ASPECTS OF THE NATIONAL DEFENSE AND SECURITY. Journal of Social and Political Sciences, Vol.3, No.3, 711-724; 2020.
FRANZ, Paulo; FERNÁNDEZ, Virginia; CODATO, Adriano. FEDERALISMO E COALIZÃO REGIONAL: A REPRESENTATIVIDADE DOS ESTADOS DA FEDERAÇÃO NOS GABINETES MINISTERIAIS BRASILEIROS. 42º Encontro Anual da ANPOCS, Caxambu-MG; 20218.
FREITAS, Carlos Eduardo de Morais. GRAUS DE COESÃO PARTIDÁRIA NO BRASIL: OS NÍVEIS DE CONVERGÊNCIA PROGRAMÁTICA DAS ELITES PARLAMENTARES SUBNACIONAIS. UFMG, Belo Horizonte-MG; 2015.
GALLAGHER, Michael. PROPORTIONALITY, DISPROPORTIONALITY AND ELECTORAL SYSTEMS. Trinity College; Dublin, Ireland; 1991.
HANDLEY, Lisa. SOME MATHEMATICAL MEASURES FOR DETERMINING IF A REDISTRICTING PLAN DISPROPORTIONALLY ADVANTAGES A POLITICAL PARTY. Michigan University, USA.
HIX, Simon; NOURY, Abdul; ROLAND, Gérard. POWER TO THE PARTIES: COHESION AND COMPETITION IN THE EUROPEAN PARLIAMENT, 1979-2001. Cambridge University Press, UK.
KESTELMAN, P. APPOTIONMENT AND PROPORTIONALITY: A MEASURED VIEW.
LAAKSO, Markku; TAAGEPERA, Rein. EFFECTIVE NUMBER OF PARTIES: A MEASURE WITH APPLICATION TO WEST EUROPE. University of California, Irvine; 1979.
MACKIE, Thomas T. UNITED KINGDOM. European Journal of Political Research, Netherlands; 1995.
MAINWARING, Scott. PRESIDENTIALISM, MULTIPARTY SYSTEMS, AND DEMOCRACY: THE DIFFICULT EQUATION. 1990.
MARTÍNEZ-PANERO, Miguel; ARREDONDO, Verónica; PEÑA, Teresa; RAMÍREZ, Victoriano. A NEW QUOTA APPROACH TO ELECTORAL DISPROPORTIONALITY. MDPI, 2019.
PAIVA, Denise; PIETRAFESA, Pedro A. SISTEMAS PARTIDÁRIOS, PARTIDOS E ELEIÇÕES. TENDÊNCIAS E DINÂMICAS NA FEDERAÇÃO BRASILEIRA 1998-2018. Puc Goiás, Brasil; 2022.
PETRY, Eric. HOW THE EFFICIENCY GAP WORKS. Brennan Center for Justice.
PIÑEIRO, Rafael. Election of Representatives and party fractionalization in Uruguay 1942-1999. Revista Uruguaya de Ciencia Política, 2004.
RIBEIRO, Pedro Floriano; LOCATELLI, Luís; ASSIS, Paulo Pedro de. ACOMPANHO O MEU PARTIDO: ORGANIZAÇÃO PARTIDÁRIA E COMPORTAMENTO LEGISLATIVO NO BRASIL. Artigos Originais; Rio de Janeiro; 2022.
ROSE, Richard. COMPARING FORMS OF COMPARATIVE ANALYSIS. Political Studies; 1991.
SATOH, Keiichi; GRONOW, Antti; YLÄ-ANTILLA, Tuomas. THE ADVOCACY COALITION INDEX: A NEW APPROACH FOR IDENTIFYING ADVOCACY COALITIONS. Policy Studies Journal; 2021.
SCHEFFLER, Iuna Lamb. DISCIPLINA PARTIDÁRIA: MENSURACÃO, TEORIA E ANÁLISE DE SEUS DETERMINANTES. UFRGS, Porto Alegre; 2019.
STEPHEN, Josh Goldenberg; FISHER, Stephen D. THE SAINTE LAGUË INDEX OF DISPROPORTIONALITY AND DALTON’S PRINCIPLE OF TRANSFERS. University of Oxford University; 2017.
SULEK, Mirosław. WIELOWYMIAROWY SPOSÓB SZACOWANIA PODSTAWOWYCH KATEGORII WOJSKOWYCH PAŃSTW. https://geopolityka.net/, 2011.
TAAGEPERA, Rein; GROFMAN, Bernard. MAPPING THE INDICES OF SEATS–VOTES DISPROPORTIONALITY AND INTER-ELECTION VOLATILITY. PARTY POLITICS VOL 9. No.6 pp. 659–677; 2013.
https://whogoverns.eu/wp-content/uploads/2021/03/Party-institutionalization-150-153.pdf. Acessado em 24 de junho de 2024.
https://whogoverns.eu/wp-content/uploads/2021/03/Closure-34-43.pdf. Acessado em 24 de junho de 2024.
https://whogoverns.eu/wp-content/uploads/2014/10/EPSA-2014.pdf. Acessado em 24 de junho de 2024.
https://whogoverns.eu/party-systems/party-system-closure/. Acessado em 24 de junho de 2024.
https://whogoverns.eu/party-systems/party-institutionalization/. Acessado em 24 de junho de 2024.
https://www.youtube.com/watch?v=yLqaVKZ4sdw&t=9s. Acessado em 3 de julho de 2024.
https://static.poder360.com.br/2023/07/Electoral_Indices_Gallagher.pdf. Acessado em 24 de junho de 2024.
https://aceproject.org/main/english/es/esg04.htm. Acessado em 24 de junho de 2024.
https://www.scielo.br/j/dados/a/DBLZXnGrZYNZRPYSKDsSGkg/. Acessado em 24 de junho de 2024.
https://www.sciencedirect.com/science/article/pii/S0895717708001933. Acessado em 24 de junho de 2024.
https://worldpopulationreview.com/country-rankings/gallagher-index-by-country. Acessado em 24 de junho de 2024.
https://onlinelibrary.wiley.com/doi/10.1111/j.1467-9248.1991.tb01622.x. Acessado em 24 de junho de 2024.
https://cran.r-project.org/web/packages/politicsR/politicsR.pdf. Acessado em 24 de junho de 2024.


